Intervalles et échelles

Les sons qui impliquent des changements de hauteur proviennent d'un grand nombre de sources et fournissent des informations utiles sur l'environnement. Pour les humains, les sources les plus importantes de changement de hauteur proviennent de la parole et de la musique. La parole comprend des schémas de hauteur ascendante et descendante qui caractérisent la prosodie vocale. Ces modèles signalent l'état émotionnel du locuteur, fournissent une source d'accent linguistique et indiquent si le locuteur pose une question ou fait une déclaration. La musique comporte également des changements de hauteur continus, mais plus souvent des changements discrets d'un niveau de hauteur à un autre, appelés intervalles. Les séquences d'intervalles caractérisent les mélodies de la musique occidentale et non occidentale et peuvent revêtir une signification structurelle, émotionnelle et esthétique importante (Crowder, 1984 ; Narmour, 1983 ; Thompson, 2009).

Tant pour la parole que pour la musique, les changements relatifs de hauteur sont très informatifs. En effet, il est possible que les changements de hauteur dans ces deux domaines soient traités par des mécanismes qui se chevauchent (Juslin & Laukka, 2003 ; Patel, 2008 ; Ross, Choi, & Purves, 2007 ; Thompson, Schellenberg, & Husain, 2004). La musique a la particularité de mettre l'accent sur une collection de catégories de hauteurs discrètes, réduisant le continuum des fréquences audibles en un nombre gérable d'éléments perceptifs et encourageant les changements brusques de hauteur. Les collections de catégories de hauteurs discrètes, ou gammes, fournissent un cadre psychologique dans lequel la musique peut être perçue, organisée, communiquée et mémorisée.

Ce chapitre examine la sensibilité humaine aux relations entre les hauteurs et les échelles musicales qui nous aident à organiser ces relations. Les systèmes d'accordage - les moyens par lesquels les échelles et les relations de hauteur sont créées et maintenues dans une tradition musicale donnée - sont également abordés. Les questions abordées dans ce chapitre sont les suivantes : Comment les intervalles de hauteur sont-ils traités par le système auditif ? Certains intervalles ont-ils un statut perceptif particulier ? Quelle est la relation entre les intervalles formés par des hauteurs sonnées séquentiellement et ceux formés par des hauteurs sonnées simultanément ? Pourquoi la plupart des musiques sont-elles organisées autour de gammes ? Existe-t-il des similitudes dans les échelles utilisées dans les différents systèmes musicaux à travers les cultures ? Existe-t-il un système d'accordage optimal ?

II. Intervalles de hauteur

Les théories sur les intervalles de hauteur dans la musique remontent au philosophe grec ionien Pythagore de Samos (~570-495 avant J.-C.). Ses idées sont ancrées dans de nombreuses discussions populaires sur la musique et ont inspiré certains compositeurs à adopter une approche purement mathématique de la composition (Navia, 1990). Bien sûr, les idées de Pythagore reflètent une explication dépassée des intervalles musicaux qui n'a pas bénéficié des avancées modernes dans l'étude de l'acoustique et du système auditif (Partch, 1974). On attribue à Pythagore la découverte que la hauteur d'une corde vibrante est directement liée à sa longueur (en supposant une tension égale), et l'idée que les intervalles musicaux correspondent à des longueurs de corde liées entre elles par des rapports entiers simples, comme 2:1 (octave), 3:2 (quinte parfaite), 4:3 (quarte parfaite) et 5:4 (tierce majeure).

Lorsque la tension est constante, la longueur d'une corde est inversement proportionnelle à la fréquence à laquelle elle vibre lorsqu'elle est pincée. Plus la corde est longue, plus elle se balance lentement d'avant en arrière lorsqu'on la pince, et plus la fréquence des vibrations sonores qui se propagent dans le système auditif est basse. De plus, comme la hauteur du son est liée à la fréquence des vibrations sonores sur une échelle logarithmique, les rapports de fréquences décrivent les mêmes intervalles musicaux quelle que soit la longueur absolue des cordes.

Galileo Galilei (1564-1642) et (indépendamment) Marin Mersenne (1588-1648) ont montré que la fréquence du mouvement vibratoire, plutôt que la longueur des cordes en soi, est légalement associée à la hauteur du son. Galileo Galilei a proposé que différentes combinaisons de sons donnent lieu à des mouvements réguliers ou irréguliers du tympan, et il a supposé que la dissonance se produit lorsque le tympan bouge de manière irrégulière. Mersenne a défini des lois pour expliquer comment on peut générer des hauteurs de son de plus en plus élevées en augmentant la tension de la corde et donc la fréquence à laquelle la corde vibre (comme dans l'accordage d'une guitare).

Ces connaissances, ainsi que d'autres découvertes de Pythagore, Galilée et Mersenne, ont ouvert la voie aux modèles psychoacoustiques contemporains de la musique. Nous savons maintenant que les propriétés acoustiques des sons sont liées à des mécanismes complexes du système auditif, façonnant conjointement notre perception et notre appréciation de la forme mélodique, de la consonance, de la dissonance et de l'harmonie (Helmholtz, 1877/1954). Pythagore avait raison de croire que certains intervalles ont un statut spécial, mais cela n'est pas vrai parce que les nombres constituent la vraie nature de toutes choses. Le statut spécial de certains intervalles émerge indirectement, reflétant une adaptation complexe du système auditif à l'environnement acoustique.

A. Intervalles simultanés

Les combinaisons de hauteurs de son simultanées sont la base de l'harmonie musicale. Pourquoi certaines combinaisons de hauteurs sonnent-elles mieux que d'autres ? La préférence pour la consonance par rapport à la dissonance est observée chez les nourrissons peu exposés à une musique culturellement spécifique (Trainor, Tsang, & Cheung, 2002 ; Hannon & Trainor, 2007). Même les poussins partagent cette tendance à préférer la consonance à la dissonance (Chiandetti & Vallortigara, 2011), bien que certains animaux non humains soient moins sensibles à cette distinction (McDermott & Hauser, 2005). Tout compte fait, il semble que les facteurs sensoriels exercent une contrainte douce sur les préférences pour la consonance, qui peut être modifiée par l'apprentissage et l'enculturation. La consonance et la dissonance jouent des rôles cruciaux dans la musique à travers les cultures : alors que la dissonance est généralement associée à la tension musicale, la consonance est généralement associée à la relaxation et à la stabilité (Butler & Daston, 1968 ; Vassilakis, 2005).

L'attrait esthétique des intervalles consonants a été remarqué très tôt par les Grecs. Pythagore a eu l'intuition que les combinaisons de hauteurs de son sont consonantes si les longueurs des cordes qui produisent les hauteurs sont liées entre elles par de petits rapports entiers. Intrigué par cette correspondance, il a défendu l'idée radicale que les nombres pouvaient expliquer l'univers (Tenney, 1988). Selon des théories plus contemporaines, la consonance perçue des intervalles est déterminée par un certain nombre de facteurs, notamment des facteurs sensoriels et acoustiques, la formation musicale, les préférences personnelles et l'enculturation (Cazden, 1945 ; Parncutt, 1989, 2006). Les résultats perceptifs des facteurs sensoriels et acoustiques sont appelés consonance et dissonance sensorielles ou psychoacoustiques ; les effets de la formation musicale, des préférences personnelles et de l'enculturation sont appelés consonance et dissonance musicales ou tonales (Terhardt, 1984).

Depuis les découvertes de Galilée et de Mersenne, la percée la plus influente dans l'étude de l'acoustique musicale a été réalisée par Helmholtz (1877/1954), qui a observé que les intervalles consonants (c'est-à-dire la consonance sensorielle) sont caractérisés par l'absence de battement. Le battement est un phénomène acoustique dans lequel des sons concomitants, similaires en fréquence mais non identiques, dérivent en phase et hors phase, de sorte que l'amplitude de la forme d'onde additionnée augmente et diminue en succession rapide. Cette oscillation entre interférence acoustique constructive et destructive est appelée battement et se produit à une vitesse déterminée par la différence entre les deux fréquences. Par exemple, en combinant les fréquences de 220 et 245, on obtient 25 battements par seconde.

La présence de battements n'entraîne pas en soi une dissonance. Des rythmes de battements très lents ne sont ni agréables ni désagréables. Selon Helmholtz, la dissonance est équivalente à la rugosité acoustique, qui se produit lorsque les battements sont si rapides qu'ils commencent à se mélanger. La rugosité et la dissonance apparaissent lorsque le rythme des battements augmente jusqu'à environ 20-30 battements par seconde, ce qui se produit lorsqu'une fréquence d'environ 400 Hz est combinée à une autre fréquence qui diffère d'environ un demi-ton (Plomp & Levelt, 1965). Plus la séparation entre deux fréquences augmente, plus le rythme des battements augmente, mais au-delà de 20-30 battements par seconde, les battements deviennent moins saillants et les deux fréquences sont perçues comme des tons distincts. Les battements disparaissent lorsque les interférences constructives et destructives ne sont plus enregistrées par le système auditif.

Cette incapacité du système auditif à enregistrer les modulations d'amplitude rapides des ondes sonores peut être expliquée en considérant la mécanique de la membrane basilaire et la façon dont elle réagit au son. Les sons purs (sons composés d'une seule fréquence) excitent des régions spécifiques de la membrane basilaire : les hautes fréquences provoquent une vibration maximale de la membrane près de la fenêtre ovale et les basses fréquences provoquent une vibration maximale de la membrane près de l'apex (Von Békésy, 1949). Deux sons purs proches en fréquence génèrent des réponses qui se chevauchent dans la membrane basilaire. Lorsque ce chevauchement a des conséquences perceptives, on dit que les fréquences se trouvent dans la même largeur de bande critique (Greenwood, 1961a, 1961b). Un chevauchement perceptiblement significatif de la réponse de la membrane basilaire à différentes fréquences entraîne des sensations de battement, de rugosité et de dissonance sensorielle. La rugosité atteint un maximum lorsque les fréquences d'entrée sont séparées d'environ 30 à 40 % d'une largeur de bande critique (Greenwood, 1991).

La largeur de la bande critique varie dans toute la gamme des fréquences audibles, qu'elle soit mesurée en hertz ou en demi-tons. Pour les hauteurs inférieures à environ 400 Hz, la largeur de la bande critique varie d'une manière qui est à peu près intermédiaire entre une échelle de fréquence linéaire (hertz) et une échelle de fréquence logarithmique (c'est-à-dire en demi-tons). Pour les hauteurs supérieures à 400 Hz, la largeur varie d'une manière proche du logarithme. Comme l'illustre la figure 1, la dissonance sensorielle devrait être évidente sur une gamme de fréquences plus large (mesurée en demi-tons) pour les basses fréquences que pour les hautes fréquences. Par exemple, un intervalle simultané de tierce majeure devrait créer moins de dissonance sensorielle lorsqu'il est joué sur les notes aiguës d'un piano que lorsqu'il est joué sur les notes graves d'un piano. Plomp et Levelt (1965) ont également noté que pour les combinaisons de sons purs, la dissonance sensorielle ne se produit que pour de petites séparations de fréquence, comme un demi-ton, et n'est pas évidente pour des intervalles plus grands.

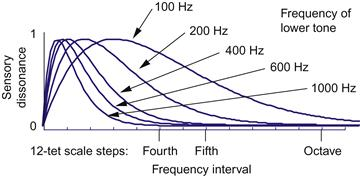
Figure 1 Dissonance sensorielle résultant d'ondes sinusoïdales simultanées. Dans la zone de hauteur supérieure, la dissonance est principalement associée à de petits intervalles. Dans la zone de hauteur inférieure, la dissonance est associée à la fois aux petits et aux grands intervalles.

Extrait de Sethares (2005, p. 47).

Les tons purs, cependant, n'existent pas dans la nature. Lorsqu'une corde est pincée, elle vibre simultanément à plusieurs fréquences, ce qui donne lieu à une forme d'onde complexe. Cette forme d'onde complexe est toujours perçue comme un ton unifié, et chaque composante de fréquence est appelée un partiel (c'est-à-dire une partie du ton). La fréquence de répétition la plus lente, ou fréquence fondamentale, est complétée par un certain nombre de fréquences de vibration plus élevées qui sont grossièrement des multiples de la fréquence fondamentale. En d'autres termes, si la fréquence fondamentale d'une corde vibrante a une valeur de f cycles par seconde (ou hertz), la corde aura également tendance à vibrer à une ou plusieurs des fréquences 2f, 3f, 4f, 5f, et ainsi de suite, créant une forme d'onde complexe.

Ces fréquences plus élevées ne sont pas entendues comme des hauteurs distinctes, mais sont regroupées avec la fréquence fondamentale et entendues comme une seule entité cohérente. En d'autres termes, le système auditif lie automatiquement les composantes de fréquence qui sont des multiples entiers d'une fréquence fondamentale commune (Micheyl & Oxenham, 2010). La hauteur d'un son complexe correspond à la fréquence de répétition globale de la forme d'onde complexe. La fréquence de répétition est généralement équivalente à la fréquence fondamentale et n'est pas affectée par la présence d'harmoniques. Elle est également la même, que la fréquence fondamentale soit présente ou non, tant qu'un certain nombre d'harmoniques sont présents. En effet, de nombreux appareils de lecture portables sont incapables de reproduire les basses fréquences et pourtant les auditeurs de ces appareils remarquent rarement que les fréquences fondamentales sont absentes (McDermott & Oxenham, 2008).

Bien que les harmoniques ne soient généralement pas entendues comme des hauteurs individuelles, elles contribuent à donner au son son timbre caractéristique ou sa qualité sonore et sont essentielles pour comprendre la nature des intervalles musicaux. La figure 2 illustre les modèles d'harmoniques évidents dans le spectre sonore d'une note jouée sur une flûte de pan avec une fréquence fondamentale de f=441 Hz et des harmoniques proéminentes aux fréquences de 3f, 5f, 7f, 9f et 11f. D'autres instruments sont associés à un modèle différent d'harmoniques. Les fréquences supérieures qui sont des multiples exacts de la fréquence fondamentale, appelées harmoniques ou partielles harmoniques, sont impliquées dans les intervalles les plus familiers de la musique. En particulier, les distances entre les partiels harmoniques sont à peu près équivalentes aux intervalles musicaux les plus connus : l'octave (f à 2f), la quinte (2f à 3f), la quarte (3f à 4f), la tierce majeure (4f à 5f), la tierce mineure (5f à 6f), la seconde majeure (8f à 9f) et la sixte majeure (3f à 5f).

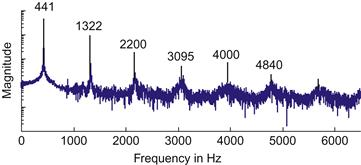
Figure 2 Le spectre d'une flûte de pan avec une fréquence fondamentale à f=440 Hz et des partiels proéminents à environ 3f, 5f, 7f, 9f et 11f.

D'après Sethares (2005, p. 111).

Il est tentant de supposer que les relations de hauteur qui se produisent entre les partiels des sons individuels sont inconsciemment intériorisées et exprimées artistiquement sous la forme de la musique et d'autres arts créatifs. Par exemple, Ross et al. (2007) ont proposé que la préférence humaine pour les intervalles les plus courants que l'on trouve dans la musique découle de l'expérience de la façon dont les formants de la parole modulent les harmoniques du larynx pour créer différents phonèmes. Leur approche a consisté à analyser les spectres des voyelles dans un discours neutre prononcé par des locuteurs d'anglais américain et de mandarin, et à comparer les harmoniques ayant la plus grande intensité dans les premiers et seconds formants. Cette procédure a donné lieu à une distribution de tous les rapports second formant/premier formant dérivés des spectres de 8 voyelles prononcées par des locuteurs d'anglais américain et de 6 voyelles prononcées par des locuteurs de mandarin. En moyenne, 68% des rapports de fréquence extraits correspondaient aux intervalles trouvés dans l'échelle chromatique. En revanche, seulement 36% des paires d'harmoniques sélectionnées au hasard dans la même gamme de fréquences correspondaient aux intervalles trouvés dans la gamme chromatique. Cette comparaison montre que les intervalles musicaux ne sont pas simplement corrélés aux intervalles de hauteur trouvés dans n'importe quelle forme d'onde harmonique (périodique), mais qu'ils reflètent un biais spécifique à la parole. Ce biais spécifique à la parole suggère que "la préférence humaine pour les intervalles spécifiques de la gamme chromatique, dont des sous-ensembles sont utilisés dans le monde entier pour créer de la musique, provient de l'expérience routinière de ces intervalles pendant la communication sociale" (Ross et al., 2007, p. 9854, voir également Han, Sundararajan, Bowling, Lake, & Purves, 2011).

La plupart des chercheurs pensent cependant que l'utilisation généralisée de certains intervalles dans la musique est encouragée par les fonctions de base du système auditif. Tout d'abord, Helmholtz (1877/1954) a noté que le concept de rugosité peut être étendu aux combinaisons de tons complexes, la quantité totale de dissonance étant égale à une combinaison de la rugosité générée par tous les partiels en interaction. Lorsque des tons avec des spectres harmoniques sont combinés, les intervalles consonants tels que l'octave et la quinte ont de nombreux partiels en commun, et ceux qui sont uniques ont tendance à ne pas se produire dans une bande critique et ne donnent donc pas lieu à une rugosité. Les tons complexes qui forment des intervalles dissonants tels que la quinte diminuée (six demi-tons) ont peu de partiels en commun, et certains de leurs partiels uniques se trouvent dans la même bande critique, ce qui donne lieu à des battements et à une rugosité. De manière plus significative, les troisième et quatrième partiels de la hauteur inférieure d'un intervalle de triton ne sont éloignés que d'un demi-ton des deuxième et troisième partiels de la hauteur supérieure de cet intervalle.

Plomp et Levelt (1965) ont calculé les niveaux prédits de consonance et de dissonance pour des combinaisons de sons constituées de six partiels harmoniques, le premier ton étant fixé à 250 Hz (voir également Hutchinson & Knopoff, 1978 ; Kameoka & Kuriyagawa, 1969a, 1969b ; Terhardt, 1974). Les résultats de ces calculs illustrent les pics de consonance aux intervalles couramment utilisés dans la musique occidentale : tierce mineure (5:6), tierce majeure (4:5), quarte parfaite (3:4), quinte parfaite (2:3), sixte majeure (3:5) et octave (1:2). Kameoka et Kuriyagawa (1969a, 1969b) ont développé un algorithme pour estimer la quantité totale de dissonance dans des dyades de sons purs et complexes. Leur modèle suppose que la dissonance est additive et dépend de l'intensité sonore, et ils se sont appuyés sur la loi de puissance de la signification psychologique pour combiner les niveaux de dissonance de différentes dyades d'harmoniques, produisant une mesure finale appelée dissonance absolue. Ces modèles mathématiques de la dissonance sont largement en accord avec les jugements de dissonance, mais les prédictions s'effondrent lorsque plus ou moins d'harmoniques sont inclus dans le modèle (Mashinter, 2006 ; Vos, 1986).

La rugosité n'est peut-être pas le seul déterminant de la consonance. Carl Stumpf (1890, 1898) a suggéré que la consonance provenait de la fusion tonale, c'est-à-dire de la tendance des combinaisons de tons à se fondre ensemble. Selon un point de vue connexe, la consonance est renforcée par l'harmonicité, c'est-à-dire la mesure dans laquelle les composantes de fréquence combinées dans un intervalle correspondent à une série harmonique unique. On pense que l'harmonicité joue un rôle important dans la perception de la hauteur. Terhardt (1974) a proposé que le système auditif fasse correspondre toute collection de partiels entrants, qu'ils proviennent d'un seul ton ou de combinaisons de tons, au modèle harmonique le plus proche. Si les partiels s'alignent sur la série harmonique, la hauteur est sans ambiguïté. Au fur et à mesure que la collection de partiels s'écarte de l'harmonique, la hauteur devient plus ambiguë.

Selon Terhardt, les modèles harmoniques se développent par l'exposition répétée aux spectres harmoniques des sons de la parole, qui prédominent dans l'environnement acoustique tout au long du développement humain. Une possibilité plus générale est que l'exposition répétée à tout stimulus acoustique entraîne le développement d'un modèle pour ce stimulus. Des modèles d'accords, par exemple, pourraient se développer même pour des combinaisons de sons qui ne correspondent pas à une série harmonique, pour autant que ces accords soient rencontrés de manière répétée dans l'environnement musical d'une personne. De tels modèles permettraient aux musiciens entraînés d'identifier des accords très familiers et pourraient également sous-tendre la perception de la consonance et de la dissonance (McLachlan ; 2011 ; voir également McLachlan & Wilson, 2010).

Pour l'intervalle d'octave, les partiels du ton le plus aigu coïncident avec les partiels pairs du ton le plus grave. Le résultat de cette combinaison est un nouveau ton complexe dont la fréquence fondamentale est égale à celle du ton inférieur d'origine, mais dont le spectre d'amplitude et, par conséquent, le timbre, sont différents. Cette coïncidence des partiels explique pourquoi les sons séparés par une octave sont perçus comme étant très similaires, un phénomène connu sous le nom d'équivalence d'octave (Idson & Massaro, 1978 ; Kallman, 1982 ; Shepard, 1964).

L'intervalle d'octave est hautement consonant et génère une forte sensation de hauteur équivalente au ton inférieur de l'intervalle. Les intervalles moins consonants ont tendance à générer des sensations de hauteur plus ambiguës. Thompson et Parncutt (1997) ont modélisé les sensations de hauteur découlant de l'intervalle de quinte parfaite, de l'intervalle de tierce majeure et de la triade majeure (voir également Parncutt, 1989). Leur modèle suppose que des intervalles simultanés génèrent de multiples sensations de hauteur qui s'étendent au-delà des fréquences fondamentales des tons, reflétant les harmoniques, les sensations de tons subharmoniques et les effets du masquage auditif. Ces sensations de hauteur varient en importance en fonction de l'intervalle, la sensation de hauteur la plus importante étant perçue comme la hauteur (virtuelle) du complexe. Les combinaisons de sons qui génèrent des sensations de hauteur hautement saillantes et non ambiguës devraient entraîner une plus grande fusion et, selon Stumpf, une plus grande consonance. Les prédictions du modèle ont été comparées aux évaluations de la qualité de l'ajustement des tonalités de sonde présentées immédiatement après les intervalles. Les résultats ont indiqué une correspondance étroite entre les prédictions et les évaluations, confirmant les hypothèses de base du modèle.

La plupart des chercheurs pensent que l'harmonique joue un rôle important dans la perception de la hauteur, mais le rôle de l'harmonique dans la consonance est moins clair. L'une des difficultés est que l'harmonicité est associée à l'absence de battement, de sorte que toute association entre l'harmonicité et la consonance peut être expliquée par la quantité de battement parmi les partiels. Pour démêler ces facteurs, McDermott, Lehr et Oxenham (2010) ont examiné les différences individuelles dans les évaluations des préférences pour les battements et l'harmonicité afin de déterminer quel facteur est le plus corrélé avec la préférence pour la consonance. De manière surprenante, leur mesure de la préférence pour les battements n'était pas bien corrélée avec les préférences pour les accords musicaux consonants et dissonants. En d'autres termes, les personnes qui trouvaient les battements désagréables n'avaient pas une aversion parallèle pour les intervalles dissonants. Au contraire, la préférence pour l'harmonicité était en bonne corrélation avec la préférence pour la consonance (voir également, Plack, 2010).

Les preuves neuroscientifiques sont également compatibles avec l'idée que l'harmonicité exerce une influence sur la consonance, du moins pour des intervalles isolés. Bidelman et Krishnan (2009) ont utilisé des potentiels liés aux événements pour indexer la consonance perçue de neuf dyades musicales. Chaque note de la dyade était un son complexe composé de six harmoniques (amplitude égale), et les intervalles du stimulus variaient en taille de 0 à 12 demi-tons (0, 1, 4, 5, 6, 7, 9, 11, 12). Les évaluations de la consonance des neuf intervalles ont également été obtenues en calculant le nombre de fois qu'un intervalle donné a été sélectionné comme ayant une "sonorité plus agréable" parmi les 36 comparaisons par paires.

Les neuf stimuli ont été présentés de manière dichotomique afin d'éviter les effets de battement et autres effets de traitement périphérique, et d'isoler les réponses des mécanismes de hauteur centrale (tronc cérébral). Les réponses de suivi de fréquence (FFR) du tronc cérébral ont ensuite été mesurées en réponse aux neuf intervalles. Le FFR reflète l'activité verrouillée en phase d'une population d'éléments neuronaux dans le mésencéphale. Elle est caractérisée par une forme d'onde périodique qui suit les cycles individuels du stimulus. Les FFR ont été analysés sur la base de leur périodicité neuronale : une valeur de saillance de hauteur neuronale a été calculée en comparant la périodicité neuronale de chaque intervalle avec un modèle de période. Cette valeur de saillance de hauteur estime la force relative des hauteurs possibles présentes dans le FFR. Par exemple, les spectres parfaitement harmoniques donnent lieu à des valeurs de saillance de hauteur élevées. Les valeurs de saillance de hauteur s'alignent étroitement avec les évaluations de consonance des intervalles (r=0,81), ce qui suggère que la consonance est fortement corrélée à la périodicité neuronale. Les intervalles de dissonance semblent être caractérisés par une périodicité neuronale moins cohérente.

Dans une étude ultérieure, Bidelman et Krishnan (2011) ont utilisé des potentiels liés aux événements pour modéliser la consonance perçue de quatre triades musicales prototypiques : triade majeure, triade mineure, triade diminuée et triade augmentée. Une fois de plus, les valeurs de saillance de la tonalité ont prédit avec précision les évaluations de consonance et de dissonance des stimuli. Les chercheurs ont affirmé que les périodes de hauteurs harmoniques produisent un haut degré de cohérence dans leur représentation neuronale, ce qui conduit à des niveaux élevés de saillance de hauteur. Les triades dissonantes, en revanche, évoquent une périodicité neuronale moins cohérente et une saillance de hauteur plus faible. Il convient toutefois de noter que les triades à forte saillance tonale sont également très courantes et donc familières. Une plus grande familiarité peut conduire à des évaluations de consonance plus élevées et à un traitement plus efficace du contenu périodique (McLachlan, 2011).

Les partiels qui sont harmoniquement liés ont tendance à fusionner, mais la fusion est également influencée par d'autres facteurs tels que les caractéristiques de coïncidence de l'apparition et du décalage. Lorsque deux tonalités différentes sont combinées pour former un intervalle, la fusion est également renforcée lorsque les tonalités ont des partiels en commun. Pour les tons complexes harmoniques, les effets de la rugosité sont corrélés à la fois avec la périodicité et la fusion, de sorte que les contributions relatives de ces facteurs à la consonance sont enchevêtrées. Une façon d'évaluer l'importance de la fusion indépendamment de la périodicité consiste à étudier la consonance des intervalles formés en combinant des sons inharmoniques. En manipulant les composantes spectrales de tons artificiels, on peut créer des intervalles qui sonnent dissonants entre les tons harmoniques mais consonants entre les tons inharmoniques. Par exemple, considérons un son complexe composé de deux partiels inharmoniques aux fréquences f et f (où la distance de f correspond à un triton, ou 6 demi-tons dans l'échelle chromatique à tempérament égal). Le spectre lui-même est inharmonique : pour la plupart des auditeurs, il ne donne pas lieu à une sensation de hauteur claire et sonne un peu comme un carillon. Néanmoins, comme le montre la figure 3, si ce carillon tritonique est combiné à un autre carillon tritonique à des distances de hauteur progressivement divergentes, la courbe dissonante théorique présentera des minima à 0 demi-ton, 6 demi-tons (l'intervalle tritonique) et 12 demi-tons (l'octave). Pour ces tailles d'intervalle, la rugosité ou le battement entre les partiels est minimisé. Ainsi, l'absence de rugosité en soi peut conduire à la perception de la consonance, même pour les spectres qui sont inharmoniques et donnent lieu à des sensations de hauteur ambiguës.

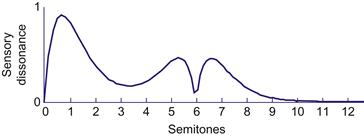
Figure 3 Courbe de dissonance pour un spectre inharmonique avec des partiels à f et f. Les minima sont évidents à 1,21 (entre 3 et 4 demi-tons) et 1,414 (un triton).

D'après Sethares (2005, p. 102).

Parmi les intervalles isolés, la consonance sensorielle peut être renforcée par la fusion tonale, l'harmonicité et l'absence de rugosité et de battement. D'autres facteurs peuvent contribuer aux aspects subtils de la perception des intervalles, comme la distinction émotionnelle entre les tierces majeures et mineures (Cook, 2007). Cependant, la musique implique rarement la présentation d'intervalles isolés, et l'influence de ces facteurs sur la consonance devient plus compliquée lorsque les intervalles sont considérés dans un contexte musical. David Huron a observé que J. S. Bach avait tendance à éviter la fusion tonale lorsqu'il recherchait (vraisemblablement) l'indépendance perceptive des voix contrapuntiques. Tout d'abord, les intervalles simultanés les plus susceptibles de fusionner, comme les octaves, les quartes, les quintes, sont généralement évités (Huron, 1991a). La stratégie compositionnelle consistant à éviter les intervalles consonants n'entraîne pas un risque accru de dissonance car les auditeurs sont encouragés à prêter attention à la structure horizontale.

Deuxièmement, lorsque des intervalles consonants sont inévitables entre différentes voix contrapuntiques, ils ont tendance à être asynchrones (Huron, 2008). Cette stratégie de composition est employée parce qu'il est difficile d'entendre les composantes individuelles d'un accord dans lequel les composantes se produisent avec des onsets et offsets synchrones (Demany & Ramos, 2005). S'il y a trop d'intervalles consonants avec des onsets synchrones, une fusion peut se produire entre des tons qui devraient être entendus comme faisant partie de différentes voix mélodiques, réduisant ainsi leur indépendance perceptive.

Comme discuté par Wright et Bregman (1987), les mécanismes de fusion tonale (structure verticale ou harmonique) peuvent s'opposer aux mécanismes de ségrégation du flux auditif qui favorisent le regroupement perceptif des tons dans le temps (structure horizontale ou mélodique). Éviter la fusion tonale peut être utilisé pour encourager la perception de la structure horizontale (voicing), et renforcer la structure horizontale (par exemple, en limitant les lignes mélodiques à de petits intervalles) peut être utilisé pour supprimer la dissonance potentielle qui pourrait se produire entre des voix simultanées dans la musique polyphonique (pour une discussion approfondie, voir Bregman, 1990, chapitre 5). De tels effets conduisent à la conclusion surprenante que la mesure dans laquelle un intervalle donné est perçu comme dissonant dépend de la façon dont les tons constitutifs sont intégrés dans les voix mélodiques respectives (Huron, 1991b). Wright (1986) a soutenu que l'augmentation historique de la dissonance perçue dans la musique correspond moins à une prévalence accrue d'harmonies dissonantes mais peut plutôt s'expliquer par une réduction des efforts visant à "préparer" les moments dissonants en mettant l'accent sur la structure horizontale.

La fusion entre intervalles simultanés peut-elle vraiment être évitée en mettant l'accent sur la structure horizontale ? Des preuves électrophysiologiques suggèrent que les mélodies simultanées sont représentées séparément dans la polyphonie à deux voix, indépendamment de la formation musicale (Fujioka, Trainor, Ross, Kakigi, & Pantev, 2005). En d'autres termes, les forces du flux auditif qui soutiennent le traitement mélodique ou "voicing" peuvent inhiber la fusion des intervalles simultanés qui sont formés lorsque les voix sont combinées (Huron, 2001). La fusion tonale ne peut cependant pas être entièrement évitée. À mesure que l'on ajoute des voix dans la polyphonie, certaines combinaisons de tons simultanés ont tendance à fusionner, ce qui entraîne une sous-estimation du nombre de voix indépendantes (Huron, 1989, voir aussi Parncutt, 1993). Dans l'homophonie, la fusion tonale est mise en avant, mais la recherche n'a pas encore établi si cette mise en avant peut inhiber complètement le traitement mélodique.

B. Intervalles séquentiels

Les intervalles formés par la succession de deux tons - également appelés intervalles mélodiques ou séquentiels - sont à la base de la mélodie. La mélodie, à son tour, joue un rôle important dans la musique. Les grands intervalles séquentiels, lorsqu'ils sont suivis d'un changement de direction, constituent la base des mélodies "de remplissage" (Meyer, 1973), et les "sauts" mélodiques sont perçus comme des points d'accent mélodique (Boltz & Jones, 1986 ; Jones, 1987). Inversement, les mélodies qui consistent en une séquence de petits intervalles semblent cohérentes et cohésives (Huron, 2001).

Les séquences d'intervalles mélodiques constituent l'"empreinte digitale" de la musique, et les procès pour violation du droit d'auteur se concentrent généralement sur la mélodie et rarement sur les attributs harmoniques, rythmiques ou timbriques de la musique (Cronin, 1997-1998 ; Frieler & Riedemann, 2011 ; Müllensiefen & Pendzich, 2009). Dans la célèbre action en justice intentée par Keith Prowse Music (KPC) contre George Harrison, alléguant une violation du droit d'auteur pour sa chanson à succès "My Sweet Lord", les arguments juridiques cruciaux portaient sur une séquence de deux intervalles descendants. Les intervalles litigieux avaient été utilisés dans une chanson populaire antérieure "He's So Fine" par les Chiffons, ainsi que d'autres détails mélodiques (Southall, 2008).

Les intervalles séquentiels ont des fonctions sensiblement différentes de celles des intervalles simultanés en musique. Dans le modèle musical implication-réalisation d'Eugene Narmour (1990, 1992), tous les modèles d'intervalles séquentiels peuvent être classés dans un ensemble de structures mélodiques de base. Puisque tout intervalle mélodique peut évoquer une "implication" pour des continuations possibles, le ton qui suit un intervalle peut être interprété comme une "réalisation" qui accomplit ou nie l'implication intervallaire initiale. Au fur et à mesure qu'une mélodie se déroule, le schéma des réalisations et des démentis des attentes intervalliques façonne la perception de la structure par l'auditeur (pour un examen et une évaluation du modèle, voir Thompson, 1996). Narmour a proposé plusieurs principes d'implication mélodique, qui ont été évalués dans un large éventail d'études empiriques (par ex, Cuddy & Lunney, 1995 ; Krumhansl, 1995a, 1995b ; Pearce & Wiggins, 2006 ; Schellenberg, 1996, 1997 ; Schellenberg, Adachi, Purdy, & McKinnon, 2002 ; Thompson, Balkwill, & Vernescu, 2000 ; Thompson, Cuddy, & Plaus, 1997 ; Thompson & Stainton, 1998). Bien que les détails des principes de Narmour aient été remis en question, les données empiriques soutiennent généralement les hypothèses essentielles du modèle d'implication-réalisation.

Les mécanismes qui sous-tendent les intervalles séquentiels et simultanés interagissent et se chevauchent. La structure horizontale (mélodique) peut être utilisée pour atténuer le niveau perçu de dissonance potentielle dans l'harmonie en cours, et les intervalles mélodiques eux-mêmes connotent des niveaux différents de consonance et de dissonance, même s'ils ne donnent pas lieu à la rugosité et au battement. En fait, l'utilisation la plus ancienne des termes consonance et dissonance faisait référence à des intervalles mélodiques successifs (Tenney, 1988).

La taille des intervalles séquentiels est généralement plus petite que celle des intervalles simultanés en musique. La figure 4 montre un histogramme de la proportion relative des différentes tailles d'intervalles de hauteur dans les mélodies occidentales, et indique que les petits intervalles (1-2 demi-tons) prédominent dans la musique classique, le rock et la musique folk. Cette caractéristique des intervalles séquentiels est due au fait que les mélodies constituent un type de flux auditif et sont soumises aux principes de ségrégation du flux auditif (Bregman, 1990). Les intervalles séquentiels au sein d'une mélodie sont généralement composés de telle sorte que les tons qui les composent sont perçus dans le même flux auditif (Huron, 2001).

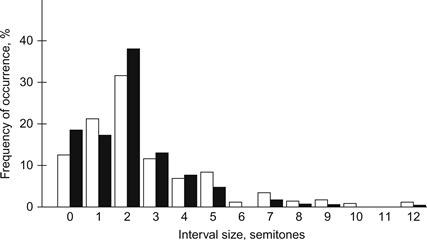
Figure 4 Histogramme montrant l'occurrence relative des intervalles de hauteur de ton de différentes tailles dans les mélodies occidentales (classique et rock : barres blanches ; folk, barres sombres).

D'après Vos et Troost (1989).

Les mécanismes neuronaux qui soutiennent le streaming auditif ne sont pas encore totalement compris, mais tout modèle complet devrait prendre en compte la ségrégation primitive et la ségrégation basée sur les schémas, y compris le rôle de l'attention (Carlyon, 2004). Bidet-Caulet et Bertrand (2009) ont proposé que les flux auditifs soient déterminés par la séparation des populations neuronales activées par des tonalités successives. Si les réponses à deux tonalités successives dépassent un certain seuil d'activation au sein de la même population neuronale, un flux est perçu ; si les réponses aux deux tonalités dépassent ce seuil d'activation dans des populations neuronales non chevauchantes, deux flux sont entendus (voir également Micheyl et al., 2007).

Dans un contexte musical, la perception et l'appréciation des intervalles mélodiques sont susceptibles d'être influencées à la fois par les mécanismes qui soutiennent le streaming auditif et par les mécanismes qui sous-tendent la consonance et la fusion pour les intervalles simultanés. Les tons qui se fondent bien ensemble en tant que simultanéité ont également tendance à bien fonctionner lorsqu'ils sont joués en séquence. Par exemple, l'intervalle simultané le plus consonant - une octave - apparaît souvent de manière mélodique, comme dans les deux premières notes de la chanson "Over the Rainbow" ou "The Christmas Song" (châtaignes grillées sur un feu ouvert). Le deuxième intervalle le plus consonant - une quinte - est très présent dans la chanson pour enfants "Twinkle Twinkle" et "Scarborough Fair" ; la tierce majeure apparaît mélodiquement dans "The Itsy-Bitsy Spider" ; la sixte majeure dans "My Bonnie" ; et la quarte parfaite dans "Oh Tannenbaum".

Cette coïncidence suggère que les mécanismes qui soutiennent la consonance et la dissonance dans des intervalles simultanés peuvent être engagés lorsque les tons de ces intervalles sont joués en séquence. Les réponses neuronales au ton initial d'un intervalle mélodique peuvent persister au-delà du décalage de ce ton (c'est-à-dire dans la mémoire de travail) et interagir avec les réponses neuronales à un ton ultérieur. Les combinaisons de sons séquentiels ne peuvent pas donner lieu à des battements et à des rugosités physiques, sauf dans des environnements hautement résonnants, comme les églises. Cependant, l'activité neuronale combinée de tonalités séquentielles se produisant dans la mémoire de travail pourrait potentiellement être soumise à des détecteurs de périodicité. Une autre explication est que l'exposition persistante à des intervalles simultanés consonants entraîne des attentes et des préférences pour ces intervalles sur le plan mélodique.

Une caractéristique qui distingue la perception des intervalles simultanés et séquentiels est que les intervalles séquentiels sont codés de deux façons (au moins) : comme une magnitude de changement de hauteur et comme un contour de hauteur. L'amplitude des intervalles séquentiels est conservée avec une grande efficacité dans la mémoire à long terme pour les mélodies familières (Attneave & Olsen, 1971 ; Dowling & Bartlett, 1981) mais est peu conservée dans la mémoire pour les mélodies nouvelles (Dowling, 1978). Le contour de la hauteur - la direction du changement d'une note à l'autre dans le temps - est important pour les mélodies nouvelles (Dowling & Fujitani, 1970 ; Edworthy, 1985). Les enfants et les nourrissons se basent également principalement sur le contour lorsqu'ils écoutent et se souviennent de mélodies (Chang & Trehub, 1977 ; Morrongiello, Trehub, Thorpe, & Capodilupo, 1985 ; Pick, Palmer, Hennessy, & Unze, 1988 ; Trehub, Bull, & Thorpe, 1984).

Il est souvent suggéré que les mécanismes qui sous-tendent le traitement de la mélodie peuvent être engagés dans des domaines autres que la musique, comme l'intonation de la parole (Ilie & Thompson, 2006, 2011 ; Miall & Dissanayake, 2003 ; Patel, 2003, 2008 ; Thompson et al., 2004 ; Thompson & Quinto, 2011). Ilie et Thompson (2006, 2011) ont constaté que les manipulations des attributs acoustiques de base tels que l'intensité, la hauteur de ton et le rythme (tempo) ont des conséquences émotionnelles similaires, qu'elles soient imposées à des stimuli musicaux ou vocaux. Thompson et al. (2004) ont montré que l'administration d'une année de cours de piano à un échantillon d'enfants entraînait une augmentation de la sensibilité aux connotations émotionnelles de la prosodie de la parole. Enfin, il existe une convergence des données statistiques sur les changements de hauteur qui se produisent dans la parole et les mélodies. Par exemple, Patel, Iversen et Rosenberg (2006) ont comparé la variabilité moyenne de la hauteur du son dans des chansons folkloriques et des discours français et anglais. Le français parlé présentait une variabilité de hauteur significativement plus faible d'une syllabe à l'autre que l'anglais parlé, et une différence parallèle a été observée pour les chansons populaires françaises et anglaises.

Les substrats neuronaux pour le traitement du contour et de la taille des intervalles semblent être différents (Liegeois-Chauvel, Peretz, Babei, Laguitton, & Chauvel, 1998 ; Peretz & Coltheart, 2003 ; Schuppert, Munte, Wieringa, & Altenmuller, 2000). Cette vision de la modularité est soutenue par les résultats de déficiences sélectives de la capacité de reconnaissance musicale après une lésion cérébrale ou chez les personnes présentant des difficultés congénitales (voir chapitre 13, ce volume). Cependant, ces dissociations ont des implications ambiguës. Par exemple, le traitement exact d'intervalles précis peut dépendre du bon fonctionnement de plusieurs calculs, de sorte qu'une lésion de l'un d'entre eux entraîne une altération de la perception des intervalles. La perception des contours peut impliquer moins de calculs ou des calculs moins précis et peut donc être moins susceptible d'être altérée après une lésion cérébrale. De plus, si l'extraction du contour a une application plus répandue que l'extraction de la taille de l'intervalle (par exemple, dans la perception de la prosodie de la parole), elle peut être robuste à la dégradation, ce qui conduit à des dissociations apparentes entre le contour et la taille de l'intervalle après une lésion cérébrale.

McDermott, Lehr et Oxenham (2008) ont démontré que la capacité d'extraire le contour est une propriété générale du système auditif. Ils ont présenté à des participants une séquence de cinq sons suivie d'une deuxième séquence transposée vers le haut ou vers le bas. Les cinq sons variaient selon l'un des trois attributs acoustiques suivants : la hauteur (comme dans une mélodie), le timbre et l'intensité. La tâche consistait à juger si le modèle de variation (contour) des deux stimuli était identique ou différent. On a constaté que les contours de timbre et d'intensité étaient reconnus tout aussi bien que les contours de hauteur, ce qui suggère que la hauteur relative n'est qu'un exemple d'une sensibilité générale aux informations relationnelles dans l'environnement acoustique. De plus, les participants pouvaient associer des contours de hauteur à des contours similaires de timbre ou d'intensité - une capacité qui peut également être étendue aux contours visuels (Prince, Schmuckler, & Thompson, 2009 ; Schmuckler, 2004). En d'autres termes, les augmentations de la luminosité et de l'intensité ont été entendues comme étant similaires aux augmentations de la hauteur du son, mais dissemblables aux diminutions de la hauteur du son (voir également Neuhoff, Kramer, & Wayand, 2002). Ces résultats suggèrent que le contour est représenté par un code général qui permet la comparaison entre différents attributs acoustiques. Une telle représentation générale serait probablement alimentée par des mécanismes de détection des changements accordés à des attributs spécifiques du son.

En ce qui concerne la hauteur, Demany, Semal et Pressnitzer (2011) ont démontré que deux types de mécanismes de détection des changements sont engagés lorsque des séquences de sons sont présentées au système auditif. L'un des mécanismes implique une comparaison implicite des informations relatives à la hauteur du son, effectuée par des détecteurs de décalage de fréquence automatiques et sensibles à la direction, et peut contribuer à une représentation du contour de la hauteur du son. L'autre implique des comparaisons explicites des tonalités et est sensible à l'ampleur d'un changement de fréquence (taille de l'intervalle). Ces deux mécanismes peuvent être impliqués dans la formation des représentations mentales des mélodies (voir également Demany, Pressnitzer, & Semal, 2009).

Compte tenu du rôle prépondérant des intervalles de hauteur dans la musique, on peut supposer que le système auditif possède une capacité spécialisée pour comparer deux sons différents sur la base de la hauteur. Pour évaluer cette possibilité, McDermott, Keebler, Micheyl et Oxenham (2010) ont examiné la précision de la perception des intervalles à l'aide d'une tâche de discrimination simple. L'acuité des intervalles a été évaluée pour trois attributs auditifs : la hauteur, la luminosité (timbre) et l'intensité sonore. Les seuils d'intervalle ont ensuite été définis par rapport aux unités de différence juste perceptible (JND) pour cet attribut (calculée comme la JND pour la discrimination de la taille de l'intervalle divisée par la JND pour la discrimination des niveaux individuels de l'attribut). Cependant, lorsque l'acuité des intervalles est calculée de cette manière, elle est en fait moins bonne pour la hauteur que pour les attributs de luminosité et d'intensité sonore. La raison principale de ce résultat est que le JND pour la hauteur était très faible, et beaucoup plus faible que pour la luminosité et l'intensité sonore. Néanmoins, ce résultat suggère que le système auditif n'est peut-être pas spécifiquement conçu pour discriminer les intervalles mélodiques en soi, mais qu'il possède des propriétés particulières qui permettent une résolution fine de la hauteur. En effet, même chez les participants entraînés à la musique, les seuils d'intervalle de hauteur étaient généralement supérieurs à un demi-ton.

Si les auditeurs sont incapables de distinguer des intervalles dont la taille diffère d'un demi-ton, comment les mélodies sont-elles perçues et mémorisées ? Le décalage de la hauteur d'une seule note d'une mélodie est très perceptible, même s'il ne modifie la hauteur originale que d'un demi-ton. Il y a plusieurs décennies, Dowling (1978) a suggéré que les mélodies non familières ne sont pas encodées comme une séquence d'intervalles mais comme un contour mélodique attaché à une gamme sous-jacente. Ce n'est que pour les mélodies familières que la taille des intervalles est retenue, et les mécanismes qui permettent leur rétention en mémoire font l'objet d'une modélisation actuelle (Deutsch, 1999 ; chapitre 7, ce volume). Étant donné l'architecture neuronale complexe du système auditif, l'abstraction d'intervalles spécifiques est possible (Deutsch, 1969). Cependant, pour les auditeurs musicalement naïfs, la capacité à percevoir et à discriminer les intervalles mélodiques peut provenir de calculs et de capacités moins spécifiques, tels que la sensibilité à gros grain à la taille de l'intervalle ou à la distance globale de la hauteur, la perception des contours, la capacité à déduire une échelle sous-jacente et la discrimination fine de la hauteur. Le démêlage de ces capacités constitue un défi important pour la construction de modèles et pour la conception d'études sur la perception des intervalles.

La nature intrigante et complexe de la perception des intervalles a été soulignée par une série d'expériences menées dans notre laboratoire (Russo & Thompson, 2005a, 2005b ; Thompson, Peter, Olsen, & Stevens (2012) ; Thompson & Russo, 2007 ; Thompson, Russo, & Livingstone, 2010). Ces études montrent que la taille perçue des intervalles mélodiques isolés dépend d'une série de facteurs contextuels tels que le timbre, l'intensité, la hauteur de ton globale et même les signaux visuels émis par les musiciens qui produisent les intervalles. Russo et Thompson (2005a) ont présenté des intervalles séquentiels ascendants et descendants à des auditeurs, qui ont évalué la taille de chaque intervalle sur une échelle de 1 à 5. Le centroïde spectral (la luminosité du timbre) de chaque ton composant l'intervalle a été manipulé pour créer des conditions congruentes et incongrues. Dans la condition congruente, le centroïde spectral des deux tons de l'intervalle reflétait la hauteur de ces tons. Par exemple, dans la condition d'intervalle ascendant, le ton initial avait un centroïde spectral plus bas et le second ton un centroïde spectral plus élevé. Dans la condition d'incongruence, le centroïde spectral des deux tons de l'intervalle était en conflit avec la hauteur de ces tons. Par exemple, dans la condition d'intervalle ascendant, le premier ton avait un centroïde spectral plus élevé et le deuxième ton un centroïde spectral plus bas. L'évaluation de la taille de l'intervalle a été influencée par le timbre des sons composants, avec des évaluations significativement plus élevées pour les conditions congruentes que pour les conditions incongruentes. Les résultats suggèrent que la hauteur et le timbre sont perçus de manière non indépendante (Garner, 1974 ; Melara & Marks, 1990), de sorte que les jugements de taille d'intervalle sont pondérés perceptivement par le contexte timbral. Une implication connexe est que les jugements de taille d'intervalle engagent un processus général d'évaluation de la distance psychologique entre les tons.

Dans une autre étude, Russo et Thompson (2005b) ont demandé à des participants entraînés et non entraînés à la musique de fournir des estimations de la magnitude de la taille d'intervalles mélodiques présentés dans un registre de hauteur élevée ou basse, en utilisant une échelle de 1 à 100. Les intervalles ascendants et descendants étaient créés en utilisant des hauteurs de son qui différaient les unes des autres de 50 cents (un demi demi-ton) à 2400 cents (deux octaves). Les participants ont ensuite été informés que les intervalles les plus petits et les plus grands devaient recevoir des valeurs de 1 et 100, respectivement. L'estimation de la taille de l'intervalle dépendait à la fois de la hauteur et de la direction de l'intervalle. Les intervalles ascendants étaient jugés plus grands que les intervalles descendants lorsqu'ils étaient présentés dans un registre de hauteur élevée, mais les intervalles descendants étaient jugés plus grands que les intervalles ascendants lorsqu'ils étaient présentés dans un registre de hauteur faible. Une interprétation de cette interaction est liée au fait que les auditeurs s'attendent à un mouvement de la hauteur des intervalles vers le centre du registre de hauteur (Huron, 2006 ; von Hippel & Huron, 2000). Un mouvement inattendu (s'éloignant du centre du registre des hauteurs) peut être perçu comme plus important qu'un mouvement vers un événement attendu, ce qui conduit à des estimations plus élevées de la taille de l'intervalle.

Nous avons également observé des effets significatifs de la formation musicale. Pour les intervalles jusqu'à une octave, la différenciation de la taille des intervalles était plus importante chez les auditeurs formés à la musique que chez les auditeurs non formés. Dans cette gamme, seuls les auditeurs entraînés ont jugé la taille de l'intervalle d'une manière cohérente avec une cartographie logarithmique de la fréquence fondamentale. Pour les intervalles supérieurs à une octave, les auditeurs entraînés et non entraînés ont montré une moindre différenciation de la taille des intervalles, et aucun des deux groupes n'a jugé les intervalles selon une cartographie logarithmique de la fréquence fondamentale. En d'autres termes, les effets de la formation musicale n'ont pas été observés pour les intervalles supérieurs à une octave, mais se sont limités aux intervalles qui apparaissent fréquemment dans la musique.

Cette divergence des jugements de taille d'intervalle par rapport à l'échelle logarithmique rappelle les premières études psychophysiques qui ont conduit à l'échelle mel. Stevens, Volkmann et Newman (1937) ont défini un son pur de 1000 Hz à 40 dB au-dessus du seuil comme 1000 mels, et la hauteur en mels d'autres fréquences a été déterminée en demandant à des participants non entraînés musicalement d'ajuster un son pur de comparaison jusqu'à ce qu'il soit perçu comme la moitié de la hauteur d'un ton standard (méthode de fractionnement). L'échelle mel et l'échelle logarithmique sont approximativement équivalentes en dessous de 500 Hz, mais elles divergent au-dessus de 500 Hz où des tailles d'intervalle perceptivement équivalentes (en mels) couvrent des rapports de fréquence progressivement plus petits (voir également Beck & Shaw, 1961 ; Greenwood, 1997 ; Stevens & Volkmann, 1940).

Le contexte tonal affecte également les jugements sur les relations entre les hauteurs. Krumhansl (1979) a demandé à des auditeurs de juger de la similarité entre des paires de tonalités présentées immédiatement après des contextes musicaux définissant des clés. En se concentrant sur les évaluations de la similarité plutôt que sur la taille de l'intervalle ou les étiquettes catégorielles, il a été possible d'obtenir des influences sur la perception des intervalles qui ne sont pas évidentes pour d'autres types de jugements. Le schéma des évaluations a révélé qu'un contexte musical affecte grandement la relation psychologique entre les tons. Les paires de tons tirés de la triade tonique de la clé de définition (premier, troisième ou cinquième degré d'une gamme majeure) ont été jugées comme étant étroitement liées. Cependant, lorsque les mêmes intervalles ne faisaient pas partie de la triade tonique, la similarité perçue entre les tons était plus faible. La similarité était également affectée par l'ordre dans lequel les tonalités étaient présentées. Les tons moins liés à la tonalité (par exemple, les tons non diatoniques) étaient jugés plus similaires aux tons stables de la tonalité (par exemple, les membres de la triade tonique) que l'ordre temporel inverse, illustrant une sorte d'effet de prototype. En bref, les intervalles sont perçus de différentes manières selon leur fonction dans un contexte tonal sous-jacent et ne dépendent pas uniquement de facteurs psychoacoustiques. Les modèles géométriques de la hauteur impliquent également qu'une description psychologique complète des relations entre les hauteurs requiert des dimensions multiples (voir également Deutsch, 1969, 1992 ; chapitre 7, ce volume ; Krumhansl, 1990 ; Krumhansl & Kessler, 1982 ; Shepard, 1964, 1982a, 1982b, 2011).

Il a souvent été suggéré que les mélodies impliquent le mouvement (Boltz, 1998 ; Jones, Moynihan, MacKenzie, & Puente, 2002 ; Repp, 1993 ; Shepard, 2011 ; Shove & Repp, 1995), et les intervalles mélodiques sont souvent décrits à l'aide de métaphores basées sur le mouvement telles que la montée et la descente. Les intervalles mélodiques ont-ils des qualités de mouvement ? Selon la théorie du codage commun, les zones de mouvement du cerveau peuvent être activées si la musique est perçue en termes d'actions sous-jacentes ou associées (Leman, 2009 ; Overy & Molnar-Szakacs, 2009 ; Prinz, 1996 ; Thompson & Quinto, 2011 ; Zatorre, Chen, & Penhune, 2007).

Des études récentes menées dans notre laboratoire par Paolo Ammirante ont démontré que les changements de hauteur de son interagissent avec les mécanismes de synchronisation dans le système moteur (Ammirante & Thompson, 2010, 2012 ; Ammirante, Thompson, & Russo, 2011). Ces études ont utilisé un paradigme de tapotement continu, dans lequel les participants tapent en synchronisation avec un signal de stimulation et tentent ensuite de continuer à tapoter à la même vitesse une fois le signal de stimulation supprimé. Pour examiner le rôle des changements de tonalité sur le système moteur, chaque tapotement dans la phase de continuation déclenchait une tonalité sonore. Les hauteurs de ces sons ont ensuite été manipulées pour former des motifs mélodiques. Les changements de tonalité affectaient systématiquement le timing des tapotements qui suivaient. Lorsqu'une tonalité déclenchée impliquait un mouvement mélodique plus rapide (des sauts mélodiques plus importants dans le même laps de temps), l'intervalle inter-tap (ITI) que la tonalité déclenchait était plus court (taps plus rapides) ; lorsqu'une tonalité déclenchée impliquait un mouvement mélodique plus lent, l'ITI était plus long. En d'autres termes, le "mouvement" mélodique implicite découlant d'intervalles de tailles différentes se reflétait dans la synchronisation des actions.

Le rôle du mouvement dans la perception des intervalles est également suggéré par mes recherches sur les expressions faciales des musiciens (Thompson & Russo, 2007 ; Thompson, Russo, & Livingstone, 2010 ; Thompson, Russo, & Quinto, 2008). Ces travaux indiquent que la perception des intervalles mélodiques est considérablement affectée par les expressions faciales des musiciens qui produisent ces intervalles. Thompson et al. (2010) ont demandé aux participants de regarder un musicien chanter un intervalle mélodique et de juger de la taille de cet intervalle sur une échelle de 1 à 7. Seul le visage du musicien était visible. Nous avons d'abord confirmé que les expressions faciales seules, même en l'absence de son, pouvaient transmettre des informations fiables sur la taille de l'intervalle mélodique chanté (voir également Thompson & Russo, 2007). Les signaux visuels et auditifs ont ensuite été manipulés de telle sorte que le signal visuel provenant d'un grand intervalle chanté soit synchronisé avec le signal auditif provenant d'un petit intervalle chanté, et vice versa. Les résultats ont confirmé que les canaux auditifs et visuels influençaient l'évaluation de la taille de l'intervalle. Des mesures faciales ont révélé que les musiciens effectuaient un certain nombre de mouvements subtils de la tête et des sourcils, auxquels les participants étaient très sensibles. Des manipulations supplémentaires ont confirmé que les informations visuelles provenant des chanteurs sont automatiquement et inconsciemment prises en compte lors de l'évaluation de la taille des intervalles. Ces résultats soulignent la nature complexe et multimodale de la perception musicale et suggèrent que les jugements analytiques des catégories d'intervalles peuvent fournir une compréhension limitée de l'expérience musicale (voir également Makeig, 1982).

C. Limites et précision de la hauteur tonale relative

Les relations de hauteur jouent un rôle central dans la perception et l'exécution de la musique : elles sont facilement perçues et mémorisées par des auditeurs avec ou sans formation musicale, et la capacité à produire des intervalles conventionnels sur un instrument de musique est une compétence de base que les musiciens acquièrent tôt dans leur formation. Dans quelle mesure les auditeurs peuvent-ils distinguer les intervalles et avec quelle précision les musiciens peuvent-ils les produire ? Certains intervalles ont-ils un statut psychologique particulier ?

L'une des limites les plus fondamentales de la perception des intervalles est la zone de hauteur. À l'extrémité inférieure du spectre audible, les intervalles sont difficiles à distinguer car de nombreux partiels de hauteurs individuelles tombent dans la même bande critique, ce qui donne lieu à des sensations de hauteurs indistinctes ou de "grondement". Au milieu de la gamme audible, les hauteurs individuelles donnent lieu à des sensations de hauteur claires et les intervalles sont facilement extraits. Les hauteurs évoquées par des sons complexes sont plus claires lorsque la fondamentale se trouve dans une région centrée sur 300 Hz (Terhardt, Stoll, & Seewann, 1982a, 1982b). Cette région de clarté de la tonalité pourrait bien influencer la pratique musicale. Huron (2001) a rapporté que la hauteur moyenne notée dans un large corpus de musique occidentale et non occidentale est approximativement D4, ce qui est très proche de la région qui évoque les sensations de hauteur les plus claires.

À l'extrémité supérieure du spectre, en particulier au-delà de 5000 Hz environ, les relations de hauteur deviennent à nouveau indistinctes (Attneave & Olson, 1971 ; Ohgushi & Hatoh, 1992 ; Semal & Demany, 1990). Une explication de cette perte de la hauteur relative est que le codage temporel de la hauteur est à la base de la perception de la musique, et non le codage spectral ou de "lieu". Le codage temporel de la hauteur, c'est-à-dire la mise à feu des neurones auditifs en phase avec la forme d'onde du stimulus, se produit jusqu'à environ 5 kHz, ce qui coïncide avec la limite supérieure de la hauteur relative (Moore, 2004 ; van Noorden, 1982). Le codage de lieu - qui est lié au lieu d'excitation maximale par les hauteurs sur la membrane basilaire - permet la discrimination des hauteurs sur une plus grande plage de fréquences. Ainsi, au-dessus de 5 kHz, où le codage temporel est absent mais où le codage de lieu demeure, les auditeurs sont toujours capables de classer les hauteurs sur une échelle allant du grave à l'aigu, mais sont incapables de différencier des intervalles spécifiques ou d'entendre des séquences de hauteurs en tant que signaux musicaux (Houtsma, 1984 ; Semal & Demany, 1990 ; Oxenham [chapitre 1, ce volume] présente une discussion approfondie des théories temporelles et de lieu de la perception des hauteurs).

Un certain nombre de méthodes psychophysiques ont été adoptées pour explorer les limites et la précision de la perception des intervalles musicaux, comme l'a largement examiné Burns (1999, voir également Zarate, Ritson, & Poeppel, 2012). Houtsma (1968) a adopté une tâche de discrimination par comparaison par paires pour estimer les JND de la taille des intervalles musicaux. Dans cette tâche, les participants se voient présenter deux intervalles et doivent indiquer lequel est le plus grand (choix forcé à deux alternatives). La hauteur du premier ton a été randomisée pour obliger les participants à baser leurs réponses sur la taille de l'intervalle plutôt que sur les valeurs absolues de la hauteur. Le JND moyen pour l'octave était de 16 cents, et les JND pour les autres intervalles de la gamme chromatique allaient de 13 à 26 cents.

Dans la méthode d'ajustement, on présente aux individus une paire de tonalités, soit en séquence, soit simultanément. L'une des tonalités est fixe et l'autre peut être ajustée. Les participants sont invités à ajuster la tonalité variable de manière à ce que la hauteur des deux tonalités corresponde à un certain intervalle. Par exemple, on peut demander à un participant d'ajuster la tonalité variable de façon à ce que l'intervalle entre les deux tonalités soit d'une octave.

Les possesseurs de hauteurs relatives sont assez cohérents entre les ajustements répétés. Pour des octaves séquentielles ou simultanées, l'écart-type intrasujet moyen des ajustements répétés est d'environ 10 cents si les deux tons sont sinusoïdaux et moins s'il s'agit de tons complexes (Burns, 1999 ; Sundberg & Lindquist, 1973 ; Terhardt, 1969 ; Ward, 1954). Sur la base de ses propres recherches et d'une revue de la recherche, Burns (1999) a conclu que lorsque les individus ajustent les tonalités pour produire un intervalle cible, il y a une tendance à comprimer les petits intervalles de quatre demi-tons ou moins (ajustement plus étroit que tempéré égal) et à étirer les grands intervalles de huit demi-tons ou plus. Cependant, ces effets dépendent de l'intervalle précis concerné. Par exemple, la compression est clairement observée pour l'intervalle de seconde mineur ascendant et descendant (Vurma & Ross, 2006) mais pas pour l'intervalle de seconde majeur (Loosen, 1993 ; Ross, 1984). La tendance à comprimer ou à étirer les intervalles dépend également de la région de fréquence dans laquelle l'intervalle est joué (Rosner, 1999).

Le phénomène d'étirement d'octave a fait l'objet d'une attention particulière (Burns, 1999 ; Dowling & Harwood, 1986). Les intervalles définis par le rapport de fréquence de 2:1 sont perçus comme étant plus petits qu'une octave, et les intervalles jugés comme étant des instances précises de l'octave sont caractérisés par des rapports de fréquence qui sont légèrement supérieurs à 2:1. Cet effet est plus évident pour les intervalles séquentiels que pour les intervalles simultanés (Burns, 1999), il est observé dans toutes les cultures (Burns, 1974) et a été confirmé à l'aide d'une série de techniques psychophysiques (Dobbins & Cuddy, 1982 ; Hartmann, 1993). Bien qu'un certain nombre d'explications aient été proposées (par exemple, Ohgushi, 1983 ; Terhardt, 1971 ; Young, 1952), le phénomène n'a pas encore été entièrement compris.

Dans l'interprétation musicale, les compétences techniques et les intentions expressives déterminent si les intervalles sont exécutés avec précision (Vurma & Ross, 2006). Pour les instruments à hauteur variable tels que le violon, l'exécution musicale implique un processus continu d'ajustement des hauteurs des sons de la musique. Ces ajustements, appelés intonation, visent souvent à rendre avec précision les intervalles notés, mais les intervalles peuvent être intentionnellement comprimés ou étirés à des fins expressives. Certains genres, comme la musique romantique, permettent une utilisation importante de l'intonation expressive, tandis que d'autres genres sont associés à une grande précision de l'intonation. Par exemple, Hagerman et Sundberg (1980) ont rapporté que la précision moyenne de l'intonation dans un échantillon de chansons barbershop expertes était inférieure à 3 cents.

L'impact esthétique de la compression ou de l'étirement des intervalles se produit sans interférer avec l'identité essentielle de ces intervalles. Ce résultat est possible principalement parce que les auditeurs s'attendent à ce que la taille des intervalles soit celle que les musiciens exécutent généralement et non celle, précise, définie par l'accord à tempérament égal (Vurma & Ross, 2006). Un autre facteur est que les auditeurs formés à la musique perçoivent les intervalles de manière catégorique (Burns, 1999 ; Burns & Ward, 1978). Deux observations soutiennent cette affirmation. Premièrement, lorsque les intervalles sont ajustés par de petites quantités pour être plus petits ou plus grands, les fonctions d'identification des auditeurs entraînés à la musique ont tendance à montrer des limites de catégorie nettes. Par exemple, si une série d'intervalles intermédiaires entre une seconde majeure et une tierce mineure est présentée, les auditeurs ont tendance à percevoir une présentation répétée du plus petit intervalle, suivie d'un changement abrupt de la catégorie d'intervalle, puis d'une présentation répétée du plus grand intervalle. Deuxièmement, si la taille de deux intervalles diffère d'une quantité fixe (par exemple, 30 cents), ils seront mieux distingués s'ils sont perçus comme appartenant à des catégories d'intervalles différentes (par exemple, tierce mineure et tierce majeure) que s'ils sont perçus comme appartenant à la même catégorie d'intervalles (deux occurrences d'une tierce majeure).

Siegel et Siegel (1977) ont utilisé l'estimation de la magnitude pour examiner la perception catégorielle des intervalles mélodiques. Six musiciens ont fourni des estimations de magnitude de 13 intervalles mélodiques dont la taille variait d'environ 6 à 8 demi-tons par incréments de 0,2 demi-ton. Tous les participants ont identifié les intervalles accordés avec une précision supérieure à 95 %. Cependant, leurs estimations d'amplitude ont révélé une capacité inégale à distinguer les intervalles. Les estimations de la magnitude de la taille des intervalles n'ont pas augmenté proportionnellement à la magnitude du stimulus, mais ont montré des étapes discrètes correspondant aux catégories d'intervalles. Ils ont également jugé que 63% des intervalles étaient "accordés", même si la plupart d'entre eux (>75%) étaient désaccordés par rapport à l'accord à tempérament égal.

La perception catégorielle a également été observée pour les intervalles simultanés. Zatorre (1983) a présenté à sept musiciens des intervalles simultanés constitués de sons purs sur une plage de 100 cents allant d'une tierce mineure (300 cents) à une tierce majeure (400 cents). L'étude a adopté un paradigme de choix forcé à deux alternatives ainsi qu'un paradigme d'identification par échelle de notation. Des effets de frontière de catégorie ont été observés en ce sens que la discrimination était meilleure pour les paires chevauchant la frontière entre deux catégories d'intervalles que pour les paires d'intervalles proches des extrémités du continuum de stimulus (voir également Zatorre & Halpern, 1979). Ces résultats montrent qu'il existe des régions le long du continuum de la taille des intervalles où la discrimination d'intervalles simultanés est améliorée, et ces régions sont associées à la présence de frontières de catégories le long de ce continuum.

À première vue, les preuves de la perception catégorielle des intervalles musicaux semblent analogues aux résultats rapportés pour les phonèmes dans la parole, mais il existe des différences notables. De manière plus significative, les catégories de la parole apparaissent très tôt dans le développement (Eimas, Siqueland, Jusczyk, & Vigorito, 1971) et les nourrissons montrent des sensibilités perceptives pour les frontières des phonèmes qui ne sont même pas utilisés dans la langue de leurs parents (Eimas & Corbit, 1973 ; Streeter, 1976). En revanche, les catégories d'intervalles musicaux ne semblent émerger qu'après une expérience ou un entraînement musical explicite. Compte tenu de ces différences, il est prématuré de conclure que les mêmes mécanismes sous-tendent les effets catégoriels dans la musique et la parole.

Les chercheurs ont également examiné la capacité des participants formés à la musique à identifier les intervalles de manière isolée ou dans un contexte musical. Taylor (1971) a présenté à des participants 25 intervalles chromatiques ascendants et descendants, y compris l'unisson. Les intervalles étaient présentés de manière isolée et intégrés dans une mélodie. Les taux d'erreur étaient plus élevés lorsque les intervalles étaient présentés dans un contexte mélodique que lorsqu'ils étaient présentés de manière isolée. De plus, le taux d'erreur n'était pas corrélé avec la force tonale des mélodies jugée subjectivement. Ces résultats sont surprenants étant donné que les contextes musicaux devraient permettre aux intervalles d'être codés à la fois comme des distances musicales (par exemple, la quarte parfaite) et comme des degrés d'une échelle sous-jacente (par exemple, de la tonique à la sous-dominante). De plus, l'entraînement musical améliore l'encodage neuronal des intervalles musicaux (Lee, Skoe, Kraus & Ashley, 2009), et la majorité du temps passé pendant l'entraînement musical implique de travailler avec des contextes musicaux complets et d'y prêter attention. Enfin, un avantage pour les intervalles isolés n'est pas observé lorsque d'autres techniques de mesure sont adoptées (Rakowski, 1990). En bref, les résultats sur la discrimination et l'identification des intervalles semblent dépendre de la méthode d'évaluation.

Une question qui se pose dans toutes les études sur la discrimination et l'identification des intervalles est de savoir s'il est raisonnable d'utiliser l'accord à tempérament égal comme norme pour classer les intervalles comme étant accordés ou désaccordés, quand on sait que l'intonation expressive s'aligne rarement précisément sur les intervalles définis par l'accord à tempérament égal. Francès (1958/1988) a comparé les taux de détection de deux types d'intervalles désaccordés dans un contexte musical. Dans une condition, les intervalles désaccordés étaient contractés ou étendus par rapport à l'accord à tempérament égal d'une manière conforme aux attentes basées sur les mesures d'intonation prises à partir de la musique jouée. Dans l'autre condition, les intervalles désaccordés étaient contractés ou étendus à l'encontre des attentes basées sur de telles mesures. Les participants étaient plus précis dans la détection des intervalles mal accordés dans la deuxième condition. Ce résultat souligne la difficulté d'établir une norme absolue permettant de définir les erreurs d'accord. Comme l'ont démontré les études psychoacoustiques de Rakowski, les intervalles mélodiques sont des entités psychologiques et leurs identités sont associées à une gamme de valeurs (Rakowski, 1976, 1982, 1985a, 1985b, 1990, 1994).

III. Gammes et systèmes d'accordage

Les intervalles mélodiques sont également fondamentaux pour les gammes - l'ensemble des hauteurs discrètes utilisées dans la plupart des musiques à travers les cultures. Quelles sont les fonctions des gammes ? L'être humain peut distinguer plus de 200 hauteurs dans une seule octave dans la gamme moyenne de l'ouïe, mais les hauteurs utilisées en musique sont généralement limitées à un petit nombre de catégories de hauteurs. Les gammes divisent le continuum des hauteurs en un nombre discret et gérable d'éléments qui sont utilisés de manière répétée. Il existe une grande diversité de gammes dans les cultures musicales, mais la plupart sont construites à partir de cinq à sept éléments par octave et permettent la formation d'un ou plusieurs intervalles consonants tels que l'octave, la quinte et la quarte. Beaucoup permettent également de différencier jusqu'à une douzaine de tailles d'intervalles différentes à l'intérieur de chaque octave. La gamme diatonique, par exemple, permet la formation d'intervalles mélodiques dont la taille varie de 1 à 12 demi-tons dans chaque octave. La présence de distinctions précises et significatives entre les tailles d'intervalle est une propriété unique de la musique. D'autres attributs du son, tels que le timbre et l'intensité, ne sont pas formellement représentés en termes de distances entre les exemplaires.

Le concept d'échelle peut être défini d'un point de vue physique, mathématique et psychologique. D'un point de vue physique, il s'agit de l'ensemble des hauteurs qui peuvent être produites sur un instrument de musique en fonction d'un certain système d'accordage. D'un point de vue mathématique, on peut utiliser une description théorique de groupe des ensembles de hauteurs comme moyen d'évaluer les ressources disponibles pour tout système de hauteurs, tel que la division en douze de l'octave à tempérament égal (Balzano, 1977, 1980, 1982). D'un point de vue psychologique, une échelle fait référence à une représentation mentale des régularités de la hauteur des sons qui est activée lorsqu'on écoute de la musique. Une telle représentation détermine, par exemple, si les tonalités entrantes sont perçues comme étant grammaticales. Elle aide également les auditeurs à déterminer les différentes fonctions des tons dans une mélodie, facilitant ainsi leur encodage en mémoire.

Les auditeurs entraînés et non entraînés extraient facilement la gamme sous-jacente de la musique, même après quelques tons seulement (Cohen, 1991). Cependant, il n'est pas certain que cette capacité à déduire la gamme sous-jacente joue un rôle important pendant l'écoute de la musique, car pratiquement toutes les personnes apprennent dès leur plus jeune âge à chanter les gammes de leur culture musicale. Il est possible que les gammes ne soient cognitivement importantes que dans la mesure où les auditeurs intériorisent la fréquence d'occurrence des hauteurs dans une tonalité établie (Oram & Cuddy, 1995 ; Krumhansl, 1985, 1990). Dans un cadre d'apprentissage statistique, il n'est pas nécessaire de supposer qu'il existe un processus spécialisé dans le cerveau qui catégorise les tonalités entrantes comme membres ou non-membres d'une gamme. Au contraire, les circuits neuronaux qui répondent à la hauteur des sons se développent d'une manière qui reflète la probabilité d'occurrence des hauteurs et des classes de hauteurs. Les notes de la gamme sont plus fréquentes que celles qui ne le sont pas, elles sont donc plus attendues et traitées plus efficacement.

En utilisant la gamme de Bohlen-Pierce non familière, Loui, Wessel et Hudson Kam (2010) ont créé des grammaires musicales à partir desquelles des mélodies ont été composées. Il y a plusieurs décennies, Heinz Bohlen a conçu la gamme de Bohlen-Pierce de manière à ce qu'elle se distingue des gammes occidentales tout en donnant un sentiment de tonalité. Les participants ont été exposés à des mélodies pendant 25 à 30 minutes et ont ensuite été évalués pour la reconnaissance, la généralisation et l'apprentissage statistique. L'apprentissage statistique a été évalué en demandant aux participants d'évaluer la qualité de l'ajustement des tons de la sonde aux mélodies de la nouvelle grammaire. Les participants, qu'ils soient ou non formés à la musique, ont pu reconnaître des mélodies individuelles avec une grande précision et ont généralisé leurs connaissances à de nouvelles mélodies composées à partir de la même grammaire. L'évaluation des tons de sonde correspondait à la fréquence d'apparition des différentes hauteurs, ce qui illustre la sensibilité aux propriétés statistiques des mélodies.

Dans un article qui a fait date, Dowling (1978) a souligné la signification psychologique des échelles. Il a présenté aux participants une mélodie cible suivie d'une mélodie de comparaison et leur a demandé d'indiquer si les mélodies étaient identiques ou différentes. Les mélodies de comparaison étaient de trois types : (a) des transpositions exactes de la mélodie cible ; (b) des transpositions conformes à l'échelle et au contour de la mélodie cible mais impliquant des changements dans les intervalles précis concernés (c'est-à-dire des réponses tonales), ou (c) des stimuli de comparaison atonaux. Les stimuli cibles correspondaient à des transpositions exactes ou à des réponses tonales, mais ils étaient rarement confondus avec des stimuli de comparaison atonaux. Sur la base de ces résultats, Dowling a proposé que les mélodies nouvelles soient principalement représentées par l'échelle et le contour, plutôt que par les intervalles précis impliqués.

La plupart des échelles occidentales et non occidentales permettent la formation d'intervalles consonants. En combinant les notes de la gamme diatonique majeure, on peut créer des intervalles tels que l'octave, la quinte, la quarte, la tierce et la sixte. Ces intervalles sont consonants principalement parce qu'ils sont représentés dans les spectres des formes d'onde périodiques complexes, y compris la voix humaine et de nombreux instruments de musique. À son tour, lorsque deux tons avec des spectres harmoniques complexes sont combinés à des distances de hauteur variables, des minima locaux de dissonance et des maxima de fusion se produisent lorsque la distance entre les tons correspond à la distance entre les partiels des spectres individuels.

L'intonation juste (accordage) est utilisée pour créer des gammes qui optimisent la consonance entre les tons de la gamme. À partir de la première note de la gamme, ou tonique, l'intonation juste optimise la consonance dans les intervalles en accordant les autres notes de la gamme de manière à ce que leurs fréquences fondamentales soient liées à celle de la tonique par de petits rapports entiers : octave (2:1), quinte (3:2), quarte (4:3), tierce majeure (5:4), tierce mineure (6:5), sixte majeure (5:3) et sixte mineure (8:5). Une des limites des échelles d'intonation juste est qu'elles sont impossibles à réaliser complètement : si le sixième degré de la gamme est accordé selon le rapport 8:5, alors l'intervalle entre le deuxième et le sixième degré de la gamme ne sera pas conforme au rapport souhaité de 3:2. Une deuxième limite des échelles de justesse est qu'elles sont intrinsèquement spécifiques à la tonalité. Elles fonctionnent bien dans la tonalité à laquelle la gamme est accordée, et dans les tonalités apparentées, mais elles sonnent de façon désagréable lorsqu'elles sont jouées dans des tonalités éloignées. Par exemple, dans une gamme de do majeur créée par un simple accord, un accord de fa majeur a un intervalle de quinte de 722 cents (environ 20 cents de plus qu'une quinte juste accordée). Bien sûr, cette préoccupation s'applique principalement aux instruments à hauteur fixe, comme le clavier, où l'accord des notes individuelles ne peut être ajusté pour convenir à une nouvelle tonalité.

Pythagore a tenté de construire une échelle musicale complète en se déplaçant successivement de haut en bas par quintes. En montant 12 fois d'un ton initial par un intervalle de quinte parfaite, on obtient un nouveau ton dont la fréquence fondamentale est liée à celle du ton initial par le rapport (3÷2)12. Ces 12 pas vers le haut ramènent à la classe de hauteur du son initial dans un système à tempérament égal (7 octaves plus haut), mais pas en intonation juste. Lorsque la hauteur définie par (3÷2)12 est transposée de sept octaves vers le bas, le rapport devient 531441÷524288, soit 23 cents d'écart par rapport à l'unisson. Cet intervalle est appelé la virgule de Pythagore et est illustré à la figure 5. L'accord à tempérament égal consiste à répartir cet écart de manière égale entre les 12 tons de la gamme chromatique. Les différences entre l'accord à tempérament égal et l'intonation juste sont subtiles mais peuvent généralement être détectées par des auditeurs attentifs. La popularité de la gamme à tempérament égal parmi les musiciens occidentaux hautement qualifiés soulève des questions sur le rôle central du battement dans la dissonance (voir également, McDermott et al., 2010).

Figure 5 La spirale des quintes, illustrant le fait qu'une gamme complète ne peut être créée en accordant progressivement les hauteurs en utilisant le rapport de fréquence 3:2. Après 12 quintes parfaites, la nouvelle hauteur est légèrement décalée de la classe de hauteur initiale d'une quantité connue sous le nom de virgule de Pythagore.

D'après Sethares (2005, p. 55).

Le tempérament égal et l'accordage juste sont conçus pour maximiser le nombre d'intervalles consonants entre les sons ayant des spectres harmoniques, y compris la voix humaine et de nombreux instruments de musique. Cependant, plusieurs types d'instruments de musique ont des timbres inharmoniques, comme les gongs, les cloches, les tambours, les bols chantants et les blocs de bois. Pour la plupart des auditeurs occidentaux, les sensations de hauteur découlant des instruments harmoniques sont plus claires que celles découlant des instruments inharmoniques, mais les deux types d'instruments peuvent être systématiquement accordés.

Les spectres des instruments qui prédominent dans une culture musicale influencent la façon dont ces instruments sont accordés et, par conséquent, les gammes qui sont associées à la musique. Sethares (2005) a noté une correspondance étroite entre les intervalles, les échelles et les propriétés spectrales des instruments. Dans les traditions qui reposent principalement sur des instruments aux spectres inharmoniques, les échelles musicales ont tendance à être très différentes des échelles diatoniques majeures et mineures occidentales, précisément parce qu'elles permettent la formation des intervalles que l'on trouve dans les spectres de ces instruments inharmoniques.

Le bonang est un instrument de musique utilisé dans le gamelan javanais et consiste en une collection de petits gongs. Selon Sethares (2005), lorsque le spectre d'un bonang est combiné à un son harmonique, il génère une courbe de dissonance dont les minima sont proches des marches d'une échelle slendro idéalisée, l'une des deux échelles essentielles de la musique gamelan. Un autre instrument utilisé dans la musique gamelan - le saron - se compose de sept barres de bronze placées sur un cadre résonnant. Lorsque le spectre du saron est combiné à un son harmonique, il génère une courbe de dissonance dont les minima sont proches des échelons de la gamme pelog, l'autre gamme essentielle de la musique gamelan.

Sur la base de ces observations, Sethares (2005) a soutenu que les instruments de musique ont évolué conjointement avec les systèmes d'accord et les échelles. Les instruments de musique qui sont joués en combinaison les uns avec les autres doivent être accordés d'une manière qui favorise leur combinaison, et cette approche de l'accordage donne naissance aux gammes qui façonnent la structure musicale. Une fois qu'un système d'accordage est établi, une tradition musicale peut également soutenir de nouveaux instruments dont les propriétés spectrales sont compatibles avec ce système d'accordage. Ce processus de coévolution explique pourquoi les échelles du gamelan et les timbres de ses instruments, qui sont si uniques, sont rarement combinés avec les échelles de la musique occidentale.

Dans les traditions qui emploient principalement des instruments à spectre harmonique, les systèmes d'accord qui permettent la formation d'intervalles consonants sont également compatibles avec les échelles pentatoniques (six notes) et heptatoniques (sept notes, diatoniques). Selon certains chercheurs et théoriciens, cette correspondance explique pourquoi les échelles pentatoniques et heptatoniques majeures et mineures sont les échelles les plus utilisées dans la musique occidentale, indienne, chinoise et arabe au cours des derniers siècles (Gill et Purves, 2009 ; Sethares, 2005).

Gill et Purves (2009) ont observé que les intervalles composants des échelles les plus utilisées à travers l'histoire et les cultures sont ceux qui présentent la plus grande similarité spectrale globale avec une série harmonique. Les intervalles dérivés des échelles possibles ont été évalués pour leur degré de similarité avec une série harmonique. La similarité a été exprimée en pourcentage de fréquences harmoniques que la dyade a en commun avec une série harmonique définie par le plus grand diviseur commun des fréquences harmoniques de la dyade.

Par exemple, si le ton supérieur d'un intervalle a des partiels à 300, 600 et 900 Hz, et que le ton inférieur a des partiels à 200, 400 et 600 Hz (quinte parfaite), alors le plus petit diviseur commun est 100 Hz. Une série harmonique avec une fréquence fondamentale à 100 Hz et la partie la plus élevée à 900 Hz (correspondant à la partie la plus élevée de la dyade) a neuf parties. Sur ces neuf partiels, six se trouvent dans la dyade. Par conséquent, le pourcentage de similitude entre la dyade et une série harmonique est de 100(6÷9)=67%.

Seuls les intervalles pouvant être produits dans une gamme d'une octave ont été analysés, et tous les intervalles pouvant être formés dans une gamme donnée ont contribué de manière égale à la valeur de similarité pour cette gamme. Comme la hauteur est un continuum et qu'il existe un nombre infini de gammes possibles, les notes de la gamme ont été limitées à 60 hauteurs possibles dans une gamme d'une octave, séparées les unes des autres par environ 20 cents (un cinquième de demi-ton). À partir de ces 60 hauteurs possibles, toutes les échelles possibles à cinq tons (pentatonique) et à sept tons (heptatonique) ont été analysées. Cette contrainte a donné lieu à 455 126 échelles pentatoniques possibles et à plus de 45 millions d'échelles heptatoniques. Parmi ce grand nombre de gammes possibles, celles qui présentaient la plus grande similitude globale avec la série harmonique étaient les gammes les plus utilisées à travers les cultures et l'histoire.

Les auteurs ont proposé qu'il existe une préférence biologique pour les séries harmoniques, et que cette préférence se reflète dans les échelles utilisées en musique. Une explication comportant moins d'hypothèses, cependant, est que les propriétés spectrales des instruments utilisés dans une tradition musicale influencent les échelles utilisées (Sethares, 2005). Étant donné qu'une grande partie des instruments produisent des sons périodiques, y compris la voix humaine, la plupart des échelles autorisent des intervalles dont les propriétés spectrales sont similaires à celles de la série harmonique (et qui présentent donc une faible dissonance). Cependant, les traditions telles que la musique javanaise gamelan qui utilisent des instruments inharmoniques ont des échelles très différentes. Les échelles slendro et pelog permettent des intervalles qui ne sont pas similaires à la série harmonique mais qui sont prévisibles à partir des propriétés spectrales des instruments utilisés dans cette tradition.

IV. Vue d'ensemble

Les changements relatifs de hauteur sont des sources d'information importantes, tant dans la musique que dans la parole. Contrairement à la parole, la musique se concentre sur une collection de hauteurs discrètes. Les combinaisons simultanées et séquentielles de ces hauteurs sont très fréquentes en musique et sont très significatives. Les intervalles simultanés diffèrent par le niveau de consonance et de dissonance qu'ils produisent. Les intervalles consonants tels que l'octave et la quinte ont de nombreux partiels en commun, et ceux qui sont uniques se situent rarement dans une bande critique et ne donnent pas lieu à une rugosité. Les facteurs sensoriels limitent les préférences pour les intervalles musicaux, mais les préférences précoces peuvent également être modifiées par l'apprentissage et l'enculturation (voir également Guernsey, 1928 ; McLachlan, 2011).

Les intervalles séquentiels constituent la base de la mélodie. Alors que les intervalles simultanés sont contraints par des processus liés à la consonance, à la dissonance et à la fusion, les intervalles séquentiels sont soumis aux contraintes du flux auditif. La musique génère des interactions significatives entre ces types d'intervalles : la fusion entre les intervalles simultanés peut être évitée en mettant l'accent sur la structure horizontale, ce qui permet aux auditeurs de percevoir des voix individuelles dans la musique polyphonique et réduit toute dissonance potentielle entre les tons simultanés.

Les mécanismes qui sous-tendent le traitement de la mélodie peuvent être utilisés dans d'autres domaines que la musique, comme l'intonation de la parole. En effet, la capacité à extraire le contour peut être une propriété générale du système auditif. On ne sait pas encore si la perception des intervalles a un statut particulier dans le système auditif. Nos perceptions des distances de hauteur dans les intervalles sont sensibles à un large éventail d'influences extérieures, notamment le timbre, le registre de hauteur, la direction du changement de hauteur, le contexte tonal et les signaux visuels provenant des interprètes. Les intervalles varient également lors de l'exécution lorsque des instruments à hauteur variable sont utilisés. Ces changements dépendent à la fois des compétences techniques et des intentions expressives des interprètes. L'intonation expressive est détectable mais ne tend pas à modifier la catégorie d'intervalle perçue.

Les échelles permettent des distinctions précises entre les tailles d'intervalles. Les auditeurs, qu'ils soient entraînés ou non, sont très sensibles aux gammes et peuvent même reconnaître une gamme sous-jacente après avoir entendu quelques notes de musique. Pendant l'écoute de la musique, cependant, la compréhension des gammes peut être moins importante que les mécanismes d'apprentissage statistique. Comme le développement des gammes dépend des timbres des instruments, il n'existe pas de gamme ou de système d'accordage idéal. Pour la musique qui met l'accent sur les instruments à spectre harmonique, les gammes tendent à permettre la formation d'intervalles tels que l'octave, la quinte et la tierce - intervalles que l'on trouve également dans le spectre harmonique des sons périodiques. Pour la musique qui met l'accent sur les instruments à spectres inharmoniques, les échelles permettent d'autres intervalles qui reflètent ces spectres. Néanmoins, la plupart des échelles à travers l'histoire et les cultures sont prévisibles à partir de la série harmonique, ce qui reflète la prévalence des spectres harmoniques dans les instruments de musique, y compris la voix humaine.