La perception de la hauteur des son

La définition d'un ton - un son périodique qui provoque une sensation de hauteur - englobe la grande majorité des sons musicaux. Les sons peuvent être soit purs - variations sinusoïdales de la pression atmosphérique à une fréquence unique - soit complexes. Les sons complexes peuvent être divisés en deux catégories : les sons harmoniques et les sons inharmoniques. Les sons complexes harmoniques sont périodiques, avec un taux de répétition appelé fréquence fondamentale (F0), et sont composés d'une somme de sinusoïdes dont les fréquences sont toutes des multiples entiers, ou harmoniques, de la F0. Les sons complexes inharmoniques sont composés de plusieurs sinusoïdes qui ne sont pas de simples multiples entiers d'une F0 commune. La plupart des sons musicaux instrumentaux ou vocaux sont plus ou moins harmoniques, mais certains, comme le carillon des cloches, peuvent être inharmoniques.

Mesure de la perception

Les attributs physiques d'un son, tels que son intensité et son contenu spectral, peuvent être facilement mesurés à l'aide d'instruments techniques modernes. Mesurer la perception du son est une autre affaire. On attribue à Gustav Fechner, un scientifique allemand du 19e siècle, la fondation du domaine de la psychophysique - la tentative d'établir une relation quantitative entre les variables physiques (par exemple, l'intensité et la fréquence du son) et les sensations qu'elles produisent (par exemple, l'intensité sonore et la hauteur du son ; Fechner, 1860). Les techniques psychophysiques qui ont été développées depuis l'époque de Fechner pour exploiter nos perceptions et nos sensations (impliquant l'audition, la vision, l'odorat, le toucher et le goût) peuvent être divisées en deux catégories de mesures, subjectives et objectives.

• Les mesures subjectives demandent généralement aux participants d'estimer ou de produire des magnitudes ou des ratios qui se rapportent à la dimension étudiée. Par exemple, pour établir une échelle d'intensité sonore, on peut présenter aux participants une série de sons de différentes intensités et leur demander d'attribuer un numéro à chaque son, correspondant à son intensité sonore. Cette méthode d'estimation de la magnitude produit ainsi une fonction psychophysique qui relie directement la sonie à l'intensité sonore.
• L'estimation du rapport suit le même principe, sauf que l'on peut présenter aux participants deux sons et leur demander de juger de combien un son est plus fort (par exemple, deux ou trois fois) que l'autre.
• Les méthodes complémentaires sont la production de magnitude et la production de ratio. Dans ces techniques de production, les participants doivent faire varier la dimension physique pertinente d'un son jusqu'à ce qu'il corresponde à une magnitude (nombre) donnée, ou jusqu'à ce qu'il corresponde à un rapport spécifique par rapport à un son de référence. Dans ce dernier cas, les instructions peuvent être du type "ajuster le niveau du deuxième son jusqu'à ce qu'il soit deux fois plus fort que le premier".

Ces quatre techniques ont été employées à de nombreuses reprises pour tenter d'établir des échelles psychophysiques appropriées (par exemple, Buus, Muesch et Florentine, 1998 ; Hellman, 1976 ; Hellman et Zwislocki, 1964 ; Stevens, 1957 ; Warren, 1970).

Parmi les autres variations de ces méthodes, citons la mise à l'échelle catégorielle et l'appariement intermodal.

La mise à l'échelle catégorielle consiste à demander aux participants de classer la sensation auditive dans une catégorie parmi un certain nombre de catégories fixes ; en suivant notre exemple d'intensité sonore, on pourrait demander aux participants de choisir une catégorie allant de très calme à très fort (par exemple, Mauermann, Long, & Kollmeier, 2004). L'appariement intermodal évite l'utilisation de chiffres en demandant, par exemple, aux participants d'ajuster la longueur d'une ligne ou d'un morceau de ficelle pour qu'elle corresponde à l'intensité sonore perçue d'un son (par exemple, Epstein & Florentine, 2005). Bien que toutes ces méthodes aient l'avantage de fournir une estimation plus ou moins directe de la relation entre le stimulus physique et la sensation, elles présentent également un certain nombre d'inconvénients. Premièrement, elles sont subjectives et reposent sur l'introspection du sujet. C'est peut-être pour cette raison qu'elles peuvent être quelque peu peu peu fiables, variables d'un participant à l'autre et au sein d'un même participant, et sujettes à divers biais (par exemple, Poulton, 1977).

L'autre approche consiste à utiliser une mesure objective, où une bonne et une mauvaise réponse peuvent être vérifiées de l'extérieur. Cette approche consiste généralement à sonder les limites de résolution du système sensoriel, en mesurant le seuil absolu (le plus petit stimulus détectable), le seuil relatif (le plus petit changement détectable dans un stimulus), ou le seuil masqué (le plus petit stimulus détectable en présence d'un autre stimulus). Il existe plusieurs façons de mesurer le seuil, mais la plupart impliquent une procédure de choix forcé, où le sujet doit choisir l'intervalle qui contient le son cible parmi une sélection de deux ou plusieurs.

Par exemple, dans une expérience mesurant le seuil absolu, on peut présenter au sujet deux intervalles de temps successifs, marqués par des lumières ; le son cible est joué pendant l'un des intervalles, et le sujet doit décider lequel c'est. On s'attendrait à ce que la performance varie en fonction de l'intensité du son : à des intensités très faibles, le son sera complètement inaudible, et la performance sera donc aléatoire (50 % d'erreurs dans une tâche à deux intervalles) ; à des intensités très élevées, le son sera toujours clairement audible, et la performance sera donc proche de 100 %, en supposant que le sujet continue à être attentif. On peut alors dériver une fonction psychométrique, qui représente la performance d'un sujet en fonction du paramètre du stimulus.

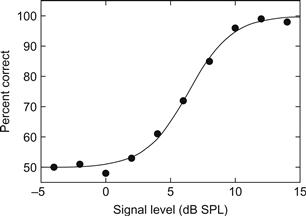
Un exemple de fonction psychométrique est illustré à la figure 1, qui représente le pourcentage de réponses correctes en fonction du niveau de pression acoustique. Ce type de paradigme à choix forcé est généralement préférable (bien que souvent plus long) à des mesures plus subjectives, telles que la méthode des limites, souvent utilisée aujourd'hui pour mesurer les audiogrammes.

Dans la méthode des limites, l'intensité d'un son est diminuée jusqu'à ce que le sujet déclare ne plus être capable de l'entendre, puis l'intensité du son est augmentée jusqu'à ce que le sujet déclare à nouveau être capable de l'entendre. L'inconvénient de ces mesures est qu'elles reposent non seulement sur la sensibilité mais aussi sur le critère - comment le sujet est prêt à déclarer avoir entendu un son s'il n'en est pas sûr. Une procédure de choix forcé élimine ce problème en obligeant les participants à deviner, même s'ils ne sont pas sûrs de l'intervalle contenant le son cible. Il est clair que le fait de tester les limites perceptives en mesurant les seuils ne nous dit pas tout sur la perception auditive humaine ; l'un des principaux problèmes est que ces mesures sont généralement indirectes - le fait de constater que les gens peuvent détecter un changement de fréquence de moins de 1% ne nous dit pas grand-chose sur la perception d'intervalles musicaux beaucoup plus grands, comme une octave. Néanmoins, elles se sont avérées extrêmement utiles pour nous aider à mieux comprendre la perception et sa relation avec la physiologie sous-jacente de l'oreille et du cerveau.

Les mesures du temps de réaction, ou temps de réponse (TR), ont également été utilisées pour étudier le traitement sensoriel. Les deux formes de base du temps de réponse sont le temps de réponse simple (TRS), où les participants doivent répondre aussi rapidement que possible en appuyant sur un seul bouton une fois qu'un stimulus est présenté, et le temps de réponse au choix (TRC), où les participants doivent classer le stimulus (généralement dans l'une des deux catégories) avant de répondre (en appuyant sur le bouton 1 ou 2).

Bien que les mesures du TR soient plus courantes dans les tâches cognitives, elles dépendent également de certains attributs sonores de base, comme l'intensité du son, les sons de plus forte intensité suscitant des réactions plus rapides, mesurées à l'aide des TRS (Kohfeld, 1971 ; Luce & Green, 1972) et des TRC (Keuss & van der Molen, 1982).

Enfin, les mesures de la perception ne se limitent pas au domaine quantitatif ou numérique. Il est également possible de demander aux participants de décrire leurs perceptions en mots. Cette approche a des applications évidentes lorsqu'il s'agit d'attributs multidimensionnels, tels que le timbre, mais elle présente également des difficultés inhérentes, car les personnes peuvent utiliser les mots descriptifs de différentes manières.

Pour résumer, la mesure de la perception est une question épineuse qui appelle de nombreuses solutions, chacune ayant ses avantages et ses inconvénients. Les mesures de la perception restent un outil d'analyse crucial au niveau des systèmes, qui peut être combiné, dans le cadre d'études sur l'homme et l'animal, à diverses techniques physiologiques et de neuro-imagerie, afin de nous aider à en savoir plus sur la façon dont les oreilles et le cerveau traitent les sons musicaux de manière à susciter les puissants effets cognitifs et émotionnels de la musique.

Perception des sons simples

Bien qu'un son unique soit loin des combinaisons complexes de sons qui composent la plupart des musiques, il peut être un point de départ utile pour comprendre comment la musique est perçue et représentée dans le système auditif. La sensation produite par un son unique est généralement divisée en trois catégories : la sonorité, la hauteur et le timbre.

L'intensité sonore

Le corrélat physique le plus évident de la sonie est l'intensité sonore (ou pression acoustique) mesurée au niveau du tympan. Cependant, de nombreux autres facteurs influencent également l'intensité sonore d'un son, notamment son contenu spectral, sa durée et le contexte dans lequel il est présenté.

La gamme dynamique et le décibel

Le système auditif humain possède une gamme dynamique énorme, le son de plus faible intensité qui est audible étant environ un facteur de 1 000 000 000 000 moins intense que le son le plus fort qui ne cause pas de dommage auditif immédiat.

Cette très large gamme est l'une des raisons pour lesquelles une échelle logarithmique - le décibel ou dB - est utilisée pour décrire le niveau sonore. Dans ces unités, la gamme dynamique de l'audition correspond à environ 120 dB. L'intensité sonore est proportionnelle au carré de la pression acoustique, qui est souvent décrite en termes de niveau de pression acoustique (SPL) en utilisant une pression, P0, de 2×10-5 N-m-2 ou 20 μPa (micropascals) comme référence, ce qui est proche du seuil absolu moyen pour les sons purs de fréquence moyenne chez les jeunes individus normo-entendants.

Le SPL d'une pression acoustique donnée, P1, est alors défini comme 20log10(P1/P0). Il existe une relation similaire entre l'intensité sonore et le niveau sonore, de sorte que le niveau est donné par 10log10(I1/I0). (Le multiplicateur est maintenant de 10 au lieu de 20 en raison de la relation de droit carré entre l'intensité et la pression). Ainsi, un niveau sonore en décibels est toujours un rapport et non une valeur absolue.

La gamme dynamique de la musique dépend du style de musique. La musique classique moderne peut avoir une gamme dynamique très étendue, depuis les passages pianissimo d'un instrument solo (environ 45 dB SPL) jusqu'à un orchestre complet jouant fortissimo (environ 95 dB SPL), tel que mesuré dans les salles de concert (Winckel, 1962). La musique pop, qui est souvent écoutée dans des conditions moins qu'idéales, comme dans une voiture ou dans la rue, a généralement une gamme dynamique beaucoup plus réduite. Les stations de radiodiffusion réduisent encore davantage la gamme dynamique en utilisant la compression pour rendre leur signal aussi fort que possible sans dépasser l'amplitude de crête maximale du canal de diffusion, de sorte que la gamme dynamique finale est rarement supérieure à environ 10 dB.

Notre capacité à distinguer de petits changements de niveau a été étudiée en profondeur pour une grande variété de sons et de conditions (par exemple, Durlach & Braida, 1969 ; Jesteadt, Wier, & Green, 1977 ; Viemeister, 1983). En règle générale, nous sommes capables de distinguer des changements de l'ordre de 1 dB, ce qui correspond à un changement de pression acoustique d'environ 12 %. Le fait que la taille de la différence juste perceptible (JND) des sons à large bande reste à peu près constante lorsqu'elle est exprimée en rapport ou en décibels est conforme à la célèbre loi de Weber, qui stipule que la JND entre deux stimuli est proportionnelle à la magnitude des stimuli.

Contrairement à notre capacité à juger des différences de niveau sonore entre deux sons présentés l'un après l'autre, notre capacité à catégoriser ou étiqueter les niveaux sonores est plutôt faible. Conformément au célèbre postulat de Miller (1956) "7 plus ou moins 2" pour le traitement de l'information et la catégorisation, notre capacité à catégoriser les niveaux sonores avec précision est assez limitée et soumise à diverses influences, comme le contexte des sons précédents. Cela peut expliquer pourquoi la notation musicale de l'intensité sonore (contrairement à la hauteur) comporte relativement peu de catégories entre le pianissimo et le fortissimo - généralement six seulement (pp, p, mp, mf, f et ff).

 

Contours d'intensité sonore égale et courbes de pondération de l'intensité sonore

Il n'y a pas de relation directe entre le niveau sonore physique (en dB SPL) et la sensation d'intensité sonore. Il y a de nombreuses raisons à cela, mais l'une des plus importantes est que l'intensité sonore dépend fortement du contenu en fréquence du son.

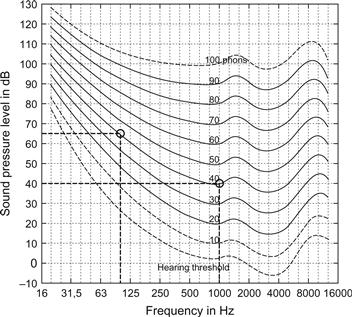
La figure 2 montre ce que l'on appelle des contours d'intensité sonore égale. Le concept de base est que deux sons purs de fréquences différentes, mais dont les niveaux se situent sur le même contour d'intensité sonore, ont la même intensité sonore. Par exemple, comme le montre la figure 2, un son pur d'une fréquence de 1 kHz et d'un niveau de 40 dB SPL a la même intensité sonore qu'un son pur d'une fréquence de 100 Hz et d'un niveau d'environ 64 dB SPL ; en d'autres termes, un son de 100 Hz doit avoir un niveau supérieur de 24 dB à celui d'un son de 40 dB SPL à 1 kHz pour être perçu comme étant aussi fort. Les contours d'intensité sonore égale sont intégrés dans une norme internationale (ISO 226) établie initialement en 1961 et révisée pour la dernière fois en 2003.

Ces contours d'intensité sonore égale ont été dérivés à plusieurs reprises de mesures psychophysiques minutieuses, avec des résultats pas toujours identiques (Fletcher & Munson, 1933 ; Robinson & Dadson, 1956 ; Suzuki & Takeshima, 2004). Les mesures impliquent généralement soit une adaptation de l'intensité sonore, où un sujet ajuste le niveau d'un son jusqu'à ce qu'il soit aussi fort qu'un second son, soit des comparaisons d'intensité sonore, où un sujet compare l'intensité sonore de plusieurs paires de sons et les résultats sont compilés pour obtenir des points d'égalité subjective (PSE). Ces deux méthodes sont très sensibles aux biais non sensoriels, ce qui rend difficile l'obtention d'un ensemble définitif de contours d'intensité sonore égale (Gabriel, Kollmeier et Mellert, 1997).

Les contours d'intensité sonore égale constituent la base de la mesure du "niveau d'intensité sonore", dont les unités sont les "phons". La valeur phon d'un son est la valeur dB SPL d'un son de 1 kHz qui est jugé avoir la même intensité sonore que le son. Ainsi, par définition, un son de 40 dB SPL à 1 kHz a un niveau sonore de 40 phons. En poursuivant l'exemple précédent, le son de 100 Hz à un niveau d'environ 64 dB SPL a également un niveau d'intensité sonore de 40 phons, car il se trouve sur le même contour d'intensité sonore que le son de 40 dB SPL à 1 kHz. Ainsi, les contours d'intensité sonore égale peuvent également être appelés contours d'égalité de phon.

Bien que les mesures réelles soient difficiles et que les résultats soient quelque peu controversés, il existe de nombreuses utilisations pratiques des contours d'intensité sonore égale. Par exemple, en ce qui concerne les nuisances sonores causées par les concerts de rock ou les aéroports, il est plus utile de connaître l'intensité perçue des sons en question que leur niveau physique. C'est pourquoi la plupart des sonomètres modernes intègrent une approximation de la courbe d'intensité sonore égale à 40 phons, appelée courbe "pondérée A". Un niveau sonore indiqué en dB (A) est un niveau sonore global qui a été filtré avec l'inverse de la courbe approximative de 40 phons. Cela signifie que les fréquences très basses et très hautes, qui sont perçues comme étant moins fortes, ont moins de poids que le milieu de la gamme de fréquences.

Comme tout outil utile, la courbe pondérée A peut être mal utilisée. Étant donné qu'elle est basée sur la courbe de 40 phons, elle convient mieux aux sons de faible niveau ; cela ne l'a toutefois pas empêchée d'être utilisée pour mesurer des sons de niveau beaucoup plus élevé, pour lesquels un filtre plus plat serait plus approprié, comme celui fourni par la courbe pondérée C, très peu utilisée. L'utilisation omniprésente de l'échelle des dB (A) pour tous les niveaux sonores est donc un exemple de cas où la commodité d'une mesure à un seul chiffre (et qui minimise l'impact des basses fréquences difficiles à contrôler) l'a emporté sur le désir de précision.

Échelles de sonie

Les contours d'intensité sonore égale et les phons nous renseignent sur la relation entre l'intensité sonore et la fréquence. En revanche, ils ne nous renseignent pas sur la relation entre l'intensité sonore et le niveau sonore. Par exemple, le phon, basé sur l'échelle des décibels à 1 kHz, ne dit rien sur l'intensité sonore d'un son de 60 dB SPL par rapport à un son de 30 dB SPL. La réponse, selon de nombreuses études sur l'intensité sonore, n'est pas deux fois plus forte. Depuis l'époque de Fechner, de nombreuses tentatives ont été faites pour établir un lien entre le niveau sonore physique et l'intensité sonore. Fechner (1860), s'appuyant sur la loi de Weber, a estimé que si les JND étaient constants sur une échelle logarithmique, et si un nombre égal de JND reflétait une variation égale de l'intensité sonore, alors l'intensité sonore devait être liée logarithmiquement à l'intensité du son.

Le psychophysicien de Harvard S. S. Stevens n'était pas d'accord, affirmant que les JND reflétaient le "bruit" dans le système auditif, ce qui ne permettait pas de comprendre directement la fonction reliant l'intensité sonore à l'intensité du son (Stevens, 1957). L'approche de Stevens a consisté à utiliser des techniques d'estimation et de production de magnitude et de rapport, telles que décrites dans la section I de ce chapitre, pour dériver une relation entre la sonie et l'intensité sonore. Il a conclu que la sonie (L) était liée à l'intensité sonore (I) par une loi de puissance :

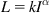
où l'exposant, α, a une valeur d'environ 0,3 aux fréquences moyennes et pour les niveaux sonores modérés et élevés.

Cette loi implique qu'une augmentation de 10 dB du niveau se traduit par un doublement de l'intensité sonore.

Aux faibles niveaux et aux fréquences plus basses, l'exposant est généralement plus grand, ce qui entraîne une fonction de croissance de la sonie plus abrupte. Stevens a utilisé cette relation pour dériver des unités d'intensité sonore, appelées "sones".

Par définition,

• 1 sone correspond à l'intensité sonore d'une tonalité de 1 kHz présentée à un niveau de 40 dB SPL
• 2 sones sont deux fois plus forts, correspondant approximativement à une tonalité de 1 kHz présentée à 50 dB SPL, et
• 4 sones correspondent à la même tonalité à environ 60 dB SPL.

 

De nombreuses études ont confirmé la conclusion de base selon laquelle la sonie peut être liée à l'intensité sonore par une loi de puissance. Cependant, en partie à cause de la variabilité des jugements de sonie et des effets substantiels de la méthodologie expérimentale (Poulton, 1979), différents chercheurs ont trouvé différentes valeurs pour l'exposant le mieux ajusté.

Par exemple, Warren (1970) a fait valoir que le fait de présenter aux participants plusieurs sons à juger entraîne invariablement un biais. Il a donc présenté à chaque sujet un seul essai. Sur la base de ces jugements à un seul essai, Warren a également dérivé une loi de puissance, mais il a trouvé une valeur d'exposant de 0,5. Cette valeur d'exposant correspond à ce que l'on pourrait attendre si l'intensité du son était proportionnelle à sa distance par rapport au récepteur, ce qui entraînerait une diminution de 6 dB du niveau pour chaque doublement de la distance. Une autre étude encore, qui a essayé d'éviter les effets de biais en utilisant toute la gamme de niveaux (100 dB) dans chaque expérience, a obtenu un exposant de seulement 0,1, ce qui implique un doublement de l'intensité sonore pour chaque augmentation de 30 dB du niveau sonore (Viemeister & Bacon, 1988).

Dans l'ensemble, il est généralement admis que la relation entre l'intensité sonore et l'intensité du son peut être approximée comme une loi de puissance, bien que des problèmes méthodologiques et la variabilité inter et intra-sujet aient rendu difficile la dérivation d'une fonction définitive et non controversée reliant la sensation à la variable physique.

Effets partiels de l'intensité sonore et du contexte

La plupart des sons que nous rencontrons, notamment en musique, sont accompagnés d'autres sons. Il est donc important de comprendre comment l'intensité sonore d'un son est affectée par le contexte dans lequel il est présenté. Dans cette section, nous traiterons de deux situations de ce type, la première étant lorsque les sons sont présentés simultanément, la seconde lorsqu'ils sont présentés séquentiellement.

Lorsque deux sons sont présentés ensemble, comme dans le cas de deux instruments de musique ou de deux voix, ils peuvent se masquer partiellement l'un l'autre, et l'intensité sonore de chacun peut ne pas être aussi élevée que si chaque son était présenté isolément. L'intensité sonore d'un son partiellement masqué est appelée "intensité partielle" (Moore, Glasberg, & Baer, 1997 ; Scharf, 1964 ; Zwicker, 1963). Lorsqu'un son est complètement masqué par un autre, sa sonorité est nulle, ou très faible. Lorsque son niveau est augmenté jusqu'à dépasser son seuil de masquage, il devient audible, mais son intensité sonore est faible - semblable à celle du même son présenté isolément, mais juste quelques décibels au-dessus de son seuil absolu. À mesure que le niveau augmente, l'intensité sonore du son augmente rapidement, rattrapant essentiellement son intensité sonore non masquée une fois qu'il se trouve à environ 20 dB ou plus au-dessus de son seuil masqué.

L'intensité sonore d'un son est également affectée par les sons qui le précèdent. Dans certains cas, les sons forts peuvent augmenter l'intensité sonore des sons qui suivent immédiatement (par exemple, Galambos, Bauer, Picton, Squires, & Squires, 1972 ; Plack, 1996) ; dans d'autres cas, l'intensité sonore des sons suivants peut être réduite (Mapes-Riordan & Yost, 1999 ; Marks, 1994).

La question de savoir si des mécanismes distincts sont nécessaires pour expliquer ces deux phénomènes fait encore débat (Arieh & Marks, 2003b ; Oberfeld, 2007 ; Scharf, Buus, & Nieder, 2002). Au départ, il n'était pas clair si le phénomène de " recalibrage de l'intensité sonore " - une réduction de l'intensité sonore des sons de niveau modéré après un son plus fort - reflétait un changement dans la façon dont les participants attribuaient des chiffres à l'intensité sonore perçue, ou reflétait un véritable changement dans la sensation d'intensité sonore (Marks, 1994). Cependant, des travaux plus récents ont montré que les temps de réponse des choix à des stimuli "recalibrés" changent d'une manière qui est cohérente avec les changements physiques de l'intensité, ce qui suggère un véritable phénomène sensoriel (Arieh & Marks, 2003a).

Modèles d'intensité sonore

Malgré les difficultés inhérentes à la mesure de la sonie, un modèle capable de prédire la sonie de sons arbitraires reste un outil utile. Le développement de modèles de perception de la sonie a une longue histoire (Fletcher & Munson, 1937 ; Moore & Glasberg, 1996, 1997 ; Moore et al., 1997 ; Moore, Glasberg, & Vickers, 1999 ; Zwicker, 1960 ; Zwicker, Fastl, & Dallmayr, 1984).

Tous reposent essentiellement sur l'idée que l'intensité sonore d'un son reflète la quantité d'excitation qu'il produit dans le système auditif. Bien qu'un test physiologique direct, comparant la quantité totale d'activité du nerf auditif dans un modèle animal avec la sonie prédite sur la base d'études humaines, n'ait pas trouvé une bonne correspondance entre les deux (Relkin & Doucet, 1997), les modèles psychophysiques qui relient les modèles d'excitation prédits, basés sur le filtrage auditif et la non-linéarité cochléaire, à la sonie fournissent généralement des prédictions précises de la sonie dans une grande variété de conditions (par exemple, Chen, Hu, Glasberg, & Moore, 2011).

Certains modèles intègrent des prédictions de sonie partielle (Chen et al., 2011 ; Moore et al., 1997), d'autres prédisent les effets de la perte d'audition cochléaire sur la sonie (Moore & Glasberg, 1997), et d'autres encore ont été étendus pour expliquer la sonie des sons qui fluctuent dans le temps (Chalupper & Fastl, 2002 ; Glasberg & Moore, 2002). Cependant, aucune de ces études n'a encore tenté d'intégrer les effets de contexte, tels que le recalibrage ou l'augmentation de la sonie.

La hauteur du son

La hauteur est sans doute la dimension la plus importante pour transmettre la musique. Les séquences de hauteurs forment une mélodie, et les combinaisons simultanées de hauteurs forment l'harmonie - deux fondements de la musique occidentale.

De nombreux ouvrages sont consacrés à la recherche sur la hauteur, tant du point de vue perceptif que neuronal (Plack, Oxenham, Popper et Fay, 2005). Le corrélat physique le plus clair de la hauteur est la périodicité, ou le taux de répétition, du son, bien que d'autres dimensions, telles que l'intensité du son, puissent avoir de petits effets (par exemple, Verschuure & van Meeteren, 1975).

Pour les jeunes ayant une audition normale, les sons purs dont la fréquence est comprise entre 20 Hz et 20 kHz environ sont audibles. Cependant, seuls les sons dont le taux de répétition se situe entre 30 Hz et 5 kHz environ suscitent une perception de la hauteur du son qui peut être qualifiée de musicale et qui est suffisamment forte pour porter une mélodie (par exemple, Attneave & Olson, 1971 ; Pressnitzer, Patterson, & Krumbholz, 2001 ; Ritsma, 1962). Il n'est peut-être pas surprenant que ces limites, qui ont été déterminées par des études psychoacoustiques, correspondent assez bien aux limites inférieures et supérieures de la hauteur de son des instruments de musique : les notes les plus basses et les plus hautes d'un piano à queue moderne, qui couvre les gammes de tous les instruments d'orchestre standard, correspondent à 27,5 Hz et 4186 Hz, respectivement.

Nous avons tendance à reconnaître les modèles de hauteurs qui forment les mélodies . Nous y parvenons vraisemblablement en reconnaissant les intervalles musicaux entre les notes successives, et la plupart d'entre nous semblent relativement insensibles aux valeurs absolues de la hauteur de la note individuelle, tant que les relations de hauteur entre les notes sont correctes. Cependant, la manière exacte dont la hauteur est extraite de chaque note et dont elle est représentée dans le système auditif reste obscure, malgré plusieurs décennies de recherches intenses.

La hauteur des sons purs

Les sons purs produisent une hauteur claire et non ambiguë, et nous sommes très sensibles aux changements de leur fréquence. Par exemple, des auditeurs bien entraînés peuvent distinguer deux sons dont la fréquence est de 1000 et 1002 Hz - une différence de seulement 0,2% (Moore, 1973).

Un demi-ton, le plus petit échelon du système d'échelle occidental, représente une différence d'environ 6 %, soit un facteur de 30 environ supérieur à la JND de fréquence pour les sons purs. Il n'est peut-être pas surprenant que les musiciens soient généralement meilleurs que les non-musiciens pour discriminer les petits changements de fréquence ; ce qui est plus surprenant, c'est qu'il ne faut pas beaucoup de pratique aux personnes sans formation musicale pour "rattraper" les musiciens en termes de performance.

Dans une étude récente, les capacités de discrimination de fréquence de musiciens classiques entraînés ont été comparées à celles d'auditeurs non entraînés sans formation musicale, en utilisant des sons purs et des sons complexes (Micheyl, Delhommeau, Perrot, & Oxenham, 2006). Au départ, les seuils étaient environ six fois plus faibles pour les auditeurs non entraînés. Cependant, il n'a fallu qu'entre 4 et 8 heures de pratique pour que les seuils des auditeurs non entraînés correspondent à ceux des musiciens entraînés, alors que les musiciens entraînés ne se sont pas améliorés avec la pratique. Ces résultats suggèrent que la plupart des gens sont capables de distinguer des différences de fréquence très fines avec très peu d'entraînement spécialisé.

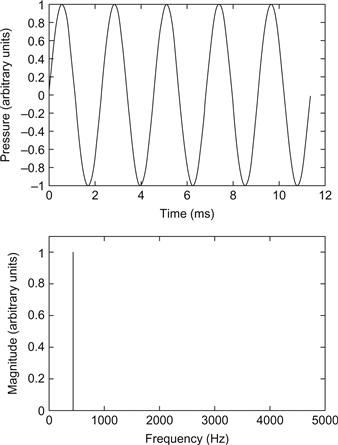
La figure 3 présente deux représentations d'un son pur à 440 Hz (le la orchestral). Le panneau supérieur montre la forme d'onde - variations de la pression acoustique en fonction du temps - qui se répète 440 fois par seconde et a donc une période de 1/440 s, soit environ 2,27 ms. Le panneau inférieur fournit la représentation spectrale, montrant que le son n'a d'énergie qu'à 440 Hz. Cette représentation spectrale correspond à un son pur "idéal", sans début ni fin.

-----------------------------------------

En pratique, l'énergie spectrale s'étend au-dessus et au-dessous de la fréquence du son pur, reflétant les effets de début et de fin. Ces deux représentations (spectrale et temporelle) constituent une bonne introduction à deux façons dont les sons purs sont représentés dans le système auditif périphérique.

Le premier code potentiel, appelé code "lieu", reflète le filtrage mécanique qui a lieu dans la cochlée de l'oreille interne. La membrane basilaire, qui s'étend de la base à l'apex de la cochlée remplie de liquide, vibre en réponse au son. Les réponses de la membrane basilaire sont très précises et très spécifiques : une certaine fréquence ne fera vibrer qu'une région locale de la membrane basilaire. En raison de ses propriétés structurelles, l'extrémité apicale de la membrane basilaire répond mieux aux basses fréquences, tandis que l'extrémité basale répond mieux aux hautes fréquences. Ainsi, chaque endroit de la membrane basilaire possède sa propre "meilleure fréquence" ou "fréquence caractéristique" (FC), c'est-à-dire la fréquence à laquelle cet endroit réagit le plus fortement. Cette correspondance entre la fréquence et le lieu, ou organisation tonotopique, est maintenue tout au long des voies auditives jusqu'au cortex auditif primaire, fournissant ainsi un code neuronal potentiel pour la hauteur des sons purs.

Le deuxième code potentiel, appelé code "temporel", repose sur le fait que les potentiels d'action, ou pointes, générés dans le nerf auditif ont tendance à se produire à une certaine phase dans la période d'une sinusoïde. Cette propriété, connue sous le nom de verrouillage de phase, signifie que le cerveau pourrait potentiellement représenter la fréquence d'un son pur par le biais des intervalles de temps entre les pointes, lorsqu'elles sont regroupées dans le nerf auditif. Aucune donnée n'est disponible pour le nerf auditif humain, en raison de la nature invasive des mesures, mais on a constaté que le verrouillage de phase s'étendait jusqu'à 2 à 4 kHz chez d'autres mammifères, selon l'espèce. Contrairement à l'organisation tonotopique, le verrouillage de phase jusqu'aux hautes fréquences n'est pas préservé dans les stations supérieures des voies auditives. Au niveau du cortex auditif, la limite du verrouillage de phase se réduit au mieux à 100 à 200 Hz (Wallace, Rutkowski, Shackleton, & Palmer, 2000). Par conséquent, la plupart des chercheurs pensent que le code temporel présent dans le nerf auditif doit être transformé en une forme de code de lieu ou de population à un stade relativement précoce du traitement auditif.

Il existe certaines preuves psychoacoustiques en faveur des codes de lieu et temporels. Une preuve en faveur d'un code temporel est que les capacités de discrimination de la hauteur du son se détériorent à des fréquences élevées : le JND entre deux fréquences devient considérablement plus grand à des fréquences supérieures à environ 4 à 5 kHz - la même gamme de fréquences au-dessus de laquelle la capacité des auditeurs à reconnaître des mélodies familières (Attneave & Olson, 1971), ou à remarquer des changements subtils dans des mélodies non familières (Oxenham, Micheyl, Keebler, Loper, & Santurette, 2011), se dégrade. Cette fréquence est similaire à celle qui vient d'être décrite, dans laquelle le verrouillage de phase dans le nerf auditif est fortement dégradé (par exemple, Palmer & Russell, 1986 ; Rose, Brugge, Anderson, & Hind, 1967), ce qui suggère que le code temporel est nécessaire pour une discrimination précise de la hauteur des sons et pour la perception des mélodies. Cela pourrait même être considéré comme une preuve que les limites supérieures de la hauteur des instruments de musique ont été déterminées par les limites physiologiques de base du nerf auditif.

La preuve de l'importance de l'information de lieu vient d'abord du fait qu'une certaine forme de perception de la hauteur reste possible même avec des sons purs de très haute fréquence (Henning, 1966 ; Moore, 1973), où il est peu probable que l'information de verrouillage de phase soit utile (par exemple, Palmer & Russell, 1986). Une autre ligne de preuves indiquant que l'information de lieu peut être importante provient d'une étude qui a utilisé ce que l'on appelle des "tonalités transposées" (van de Par & Kohlrausch, 1997) pour présenter l'information temporelle qui ne serait normalement disponible que pour une région à basse fréquence de la cochlée à une région à haute fréquence, dissociant ainsi les indices temporels des indices de lieu (Oxenham, Bernstein, & Penagos, 2004). Dans cette étude, la discrimination de la hauteur du son était considérablement plus mauvaise lorsque les informations temporelles à basse fréquence étaient présentées au " mauvais " endroit dans la cochlée, ce qui suggère que les informations de lieu sont importantes.

À la lumière de ces données contradictoires, il est peut-être plus sûr de supposer que le système auditif utilise à la fois les informations de lieu et de temps du nerf auditif afin d'extraire la hauteur des sons purs. En effet, certaines théories de la hauteur nécessitent explicitement des informations précises sur le lieu et le moment (Loeb, White, & Merzenich, 1983). Mieux comprendre comment ces informations sont extraites reste un objectif de recherche important. La question est particulièrement pertinente sur le plan clinique, car les déficits de perception de la hauteur du son sont fréquents chez les malentendants et les porteurs d'implants cochléaires. Une meilleure compréhension de la façon dont le cerveau utilise les informations provenant de la cochlée aidera les chercheurs à améliorer la façon dont les prothèses auditives, telles que les appareils auditifs et les implants cochléaires, présentent les sons à leurs utilisateurs.

2. La hauteur des sons complexes

Une grande majorité des sons musicaux sont des sons complexes d'une forme ou d'une autre, et la plupart d'entre eux sont associés à une hauteur. Les sons complexes harmoniques sont les plus courants. Ils sont composés de la fréquence F0 (correspondant au taux de répétition de la forme d'onde entière) et des partiels supérieurs, harmoniques ou harmoniques, espacés de multiples entiers de la fréquence F0. La hauteur d'un son complexe harmonique correspond généralement au F0. En d'autres termes, si l'on demande à un sujet de faire correspondre la hauteur d'un son complexe à celle d'un son pur unique, la meilleure correspondance se produit généralement lorsque la fréquence du son pur est la même que la F0 du son complexe. Il est intéressant de noter que cela est vrai même lorsque le son complexe n'a pas d'énergie à la F0 ou que la F0 est masquée (de Boer, 1956 ; Licklider, 1951 ; Schouten, 1940 ; Seebeck, 1841). Ce phénomène a été désigné par différents termes, dont la hauteur du fondamental manquant, la hauteur de périodicité, la hauteur de résidu et la hauteur virtuelle. La capacité du système auditif à extraire la F0 d'un son est importante du point de vue de la constance perceptive : imaginez qu'une note de violon soit jouée dans une pièce calme, puis à nouveau dans une pièce équipée d'un système de climatisation bruyant. Le bruit à basse fréquence du système de climatisation pourrait bien masquer une partie de l'énergie à basse fréquence du violon, y compris la F0, mais nous ne nous attendrions pas à ce que la hauteur (ou l'identité) du violon change à cause de cela.

Bien que la capacité d'extraire la hauteur de la périodicité soit clairement importante et partagée par de nombreuses espèces différentes (Shofner, 2005), la manière exacte dont le système auditif extrait la F0 reste en grande partie inconnue. Les étapes initiales du traitement d'un son complexe harmonique sont illustrées à la figure 4. Les deux panneaux supérieurs montrent la forme d'onde temporelle et la représentation spectrale d'un son complexe harmonique. Le troisième panneau décrit le filtrage qui se produit dans la cochlée : chaque point de la membrane basilaire peut être représenté comme un filtre passe-bande qui ne répond qu'aux fréquences proches de sa fréquence centrale. Le quatrième panneau montre le "modèle d'excitation" produit par le son. Il s'agit de la réponse moyenne de la banque de filtres passe-bande, représentée en fonction de la fréquence centrale des filtres (Glasberg & Moore, 1990). Le cinquième panneau montre un extrait de la forme d'onde temporelle à la sortie de certains des filtres du réseau. Il s'agit d'une approximation de la forme d'onde qui entraîne les cellules ciliées internes de la cochlée, qui à leur tour font synapse avec les fibres nerveuses auditives pour produire les trains de pointes que le cerveau doit interpréter.

Figure 4 Représentations d'un son complexe harmonique dont la fréquence fondamentale (F0) est de 440 Hz. Le panneau supérieur montre la forme d'onde temporelle. Le deuxième panneau montre le spectre de puissance de la même forme d'onde. Le troisième panneau montre le banc de filtres auditifs, représentant le filtrage qui se produit dans la cochlée. Le quatrième panneau montre le modèle d'excitation, ou la moyenne temporelle de la sortie du banc de filtres. Le cinquième panneau montre quelques échantillons de formes d'onde temporelles à la sortie du banc de filtres, y compris des filtres centrés sur le F0 et la quatrième harmonique, illustrant des harmoniques résolus, et des filtres centrés sur les 8e et 12e harmoniques du complexe, illustrant des harmoniques qui sont moins bien résolus et présentent des modulations d'amplitude à un taux correspondant au F0.

Si l'on considère les deux panneaux inférieurs de la figure 4, il est possible d'observer une transition entre les harmoniques de faible numérotation à gauche et les harmoniques de numérotation élevée à droite : Les premières harmoniques génèrent des pics distincts dans le schéma d'excitation, car les filtres dans cette région de fréquence sont plus étroits que l'espacement entre les harmoniques successives. Notez également que les formes d'onde temporelles aux sorties des filtres centrés sur les harmoniques à faible numérotation ressemblent à des tons purs. À des nombres d'harmoniques plus élevés, la largeur de bande des filtres auditifs devient plus large que l'espacement entre les harmoniques successives, et les pics individuels dans le modèle d'excitation sont donc perdus. De même, la forme d'onde temporelle à la sortie des filtres à haute fréquence ne ressemble plus à un ton pur, mais reflète l'interaction de plusieurs harmoniques, produisant une forme d'onde complexe qui se répète à un rythme correspondant à la F0.

Les harmoniques qui produisent des pics distincts dans le schéma d'excitation et/ou produisent des vibrations quasi-sinusoïdales sur la membrane basilaire sont dites "résolues". D'un point de vue phénoménologique, les harmoniques résolues sont celles qui peuvent être "entendues" comme des tons séparés dans certaines circonstances. En général, nous n'entendons pas les harmoniques individuelles lorsque nous écoutons un son musical, mais notre attention peut être attirée sur elles de différentes manières, par exemple en les amplifiant ou en les activant et désactivant alors que les autres harmoniques restent continues (par exemple, Bernstein & Oxenham, 2003 ; Hartmann & Goupell, 2006). La capacité de résoudre ou d'entendre les harmoniques individuelles à faible numérotation comme des sons purs a déjà été notée par Hermann von Helmholtz dans son ouvrage classique, On the Sensations of Tone Perception (Helmholtz, 1885/1954).

Les harmoniques supérieures, qui ne produisent pas de pics d'excitation individuels et ne peuvent généralement pas être entendues, sont souvent qualifiées de "non résolues". On pense que la transition entre les harmoniques résolues et non résolues se situe quelque part entre la 5e et la 10e harmonique, en fonction de divers facteurs, tels que la F0 et les amplitudes relatives des composantes, ainsi que de la façon dont la résolvabilité est définie (par exemple, Bernstein & Oxenham, 2003 ; Houtsma & Smurzynski, 1990 ; Moore & Gockel, 2011 ; Shackleton & Carlyon, 1994).

De nombreuses théories et modèles ont été élaborés pour expliquer comment la hauteur est extraite des informations présentes dans la périphérie auditive (de Cheveigné, 2005). Comme pour les sons purs, les théories peuvent être divisées en deux catégories de base : les théories de lieu et les théories temporelles.

Les théories de lieu proposent généralement que le système auditif utilise les harmoniques résolues d'ordre inférieur pour calculer la hauteur (par exemple, Cohen, Grossberg, & Wyse, 1995 ; Goldstein, 1973 ; Terhardt, 1974b ; Wightman, 1973). Cela pourrait se faire par le biais d'un processus de correspondance de modèles, avec soit des modèles harmoniques "câblés", soit des modèles qui se développent par l'exposition répétée à des séries harmoniques, qui finissent par être associés à la F0.

Les théories temporelles impliquent généralement l'évaluation des intervalles de temps entre les pointes de l'oreille, en utilisant une forme d'autocorrélation ou un histogramme de pointes tout-intervalle (Cariani & Delgutte, 1996 ; Licklider, 1951 ; Meddis & Hewitt, 1991 ; Meddis & O'Mard, 1997 ; Schouten, Ritsma, & Cardozo, 1962). Cette information peut être obtenue à partir des harmoniques résolues et non résolues. La mise en commun de ces pointes provenant de l'ensemble du réseau nerveux permet l'émergence d'un intervalle dominant qui correspond à la période de la forme d'onde (c'est-à-dire l'inverse de la F0).

Une troisième solution consiste à utiliser à la fois les informations de lieu et de temps. Dans une version, la coïncidence temporelle entre les neurones dont les FC sont harmoniquement liées est supposée conduire à un réseau spatial de détecteurs de coïncidence - un modèle basé sur le lieu qui émerge grâce aux informations temporelles coïncidentes (Shamma & Klein, 2000).

Dans une autre version, le temps de réponse aux impulsions des filtres auditifs, qui dépend de la FC, est supposé déterminer la gamme de périodicités qu'un certain emplacement tonotopique peut coder (de Cheveigné & Pressnitzer, 2006). Des études physiologiques récentes ont soutenu au moins la plausibilité des mécanismes lieu-temps pour coder la hauteur du son (Cedolin & Delgutte, 2010).

Il s'est avéré très difficile de faire la distinction entre les modèles spatio-temporels (ou spatio-temporels) de la hauteur du son. Cela est dû en partie au fait que les représentations spectrales et temporelles d'un signal sont mathématiquement équivalentes : tout changement dans la représentation spectrale entraîne automatiquement un changement dans la représentation temporelle, et vice versa. Les tentatives psycho-acoustiques de distinguer les mécanismes de lieu et de temps se sont concentrées sur les limites imposées par la physiologie périphérique de la cochlée et du nerf auditif.

Par exemple, les limites de la sélectivité fréquentielle peuvent être utilisées pour tester la théorie du lieu : si toutes les harmoniques sont clairement non résolues (et ne fournissent donc aucune information sur le lieu) et qu'une hauteur est quand même entendue, alors la hauteur ne peut pas dépendre uniquement de l'information sur le lieu. De même, les limites supposées du verrouillage de phase peuvent être utilisées : si la périodicité de la forme d'onde et les fréquences de toutes les harmoniques résolues sont toutes supérieures à la limite du verrouillage de phase dans le nerf auditif et qu'une hauteur est toujours entendue, il est peu probable que des informations temporelles soient nécessaires à la perception de la hauteur.

Un certain nombre d'études ont montré que la perception de la hauteur du son est possible même lorsque les complexes de sons harmoniques sont filtrés pour éliminer toutes les harmoniques résolues de faible numérotation (Bernstein & Oxenham, 2003 ; Houtsma & Smurzynski, 1990 ; Kaernbach & Bering, 2001 ; Shackleton & Carlyon, 1994). Une conclusion similaire a été atteinte par des études qui ont utilisé un bruit large bande modulé en amplitude, qui ne présente pas de pics spectraux dans son spectre à long terme (Burns & Viemeister, 1976, 1981). Ces résultats suggèrent que la hauteur du son peut être extraite uniquement de l'information temporelle, ce qui exclut les théories qui ne prennent en compte que le codage de lieu. Cependant, la sensation de hauteur produite par des harmoniques non résolues ou par un bruit modulé est relativement faible par rapport à la hauteur des instruments de musique, qui produisent des sons complexes entièrement harmoniques.

La tonalité la plus saillante que nous associons normalement à la musique est fournie par les harmoniques résolues de rang inférieur. Les études qui ont examiné les contributions relatives des harmoniques individuelles ont montré que les harmoniques 3 à 5 (Moore, Glasberg, & Peters, 1985), ou les fréquences autour de 600 Hz (Dai, 2000), semblent avoir le plus d'influence sur la hauteur du complexe global. C'est là que les modèles temporels actuels rencontrent également quelques difficultés : ils sont capables d'extraire la F0 d'un son complexe aussi bien à partir d'harmoniques non résolues qu'à partir d'harmoniques résolues, et par conséquent, ils ne prédisent pas la grande différence de saillance et de précision de la hauteur entre les harmoniques à faible et à fort numéro qui est observée dans les études psychophysiques (Carlyon, 1998). En d'autres termes, les modèles de lieu ne prédisent pas une performance suffisamment bonne avec des harmoniques non résolues, alors que les modèles temporels prédisent une performance trop bonne. La différence apparemment qualitative et quantitative de la hauteur produite par les harmoniques à nombre faible et à nombre élevé a conduit à suggérer que deux mécanismes de hauteur pourraient être à l'œuvre, l'un pour coder le taux de répétition de l'enveloppe temporelle des harmoniques à nombre élevé et l'autre pour coder la F0 des harmoniques individuelles à nombre faible (Carlyon & Shackleton, 1994), bien que des travaux ultérieurs aient remis en question certaines des preuves proposées pour les deux mécanismes (Gockel, Carlyon, & Plack, 2004 ; Micheyl & Oxenham, 2003).

Le fait que les harmoniques résolues et de faible numérotation soient importantes suggère que le codage du lieu peut jouer un rôle dans la tonalité quotidienne. D'autres preuves proviennent de diverses études. L'étude mentionnée précédemment qui utilisait des sons avec des informations temporelles de basse fréquence transposées dans une gamme de haute fréquence (Oxenham et al., 2004) a étudié la perception de la hauteur des sons complexes en transposant les informations des harmoniques 3, 4 et 5 d'une F0 de 100 Hz dans des régions de haute fréquence de la cochlée - environ 4 kHz, 6 kHz et 10 kHz. Si l'information temporelle était suffisante pour susciter une hauteur de périodicité, alors les auditeurs auraient dû être capables d'entendre une hauteur correspondant à 100 Hz. En fait, aucun des auditeurs n'a rapporté avoir entendu une tonalité basse ou n'a été capable de faire correspondre la tonalité des tons transposés à celle de la fondamentale manquante. Cela suggère que, si des informations temporelles sont utilisées, elles doivent être présentées à l'endroit "correct" de la cochlée.

Une autre ligne de preuve est venue du réexamen des premières conclusions selon lesquelles aucune hauteur de son n'est entendue lorsque toutes les harmoniques sont supérieures à environ 5 kHz (Ritsma, 1962). Cette première conclusion a conduit les chercheurs à suggérer que l'information sur la périodicité était cruciale et qu'à des fréquences supérieures aux limites du verrouillage de phase, la hauteur de la périodicité n'était pas perçue. Une étude récente est revenue sur cette conclusion et a constaté qu'en fait, les auditeurs étaient bien capables d'entendre les hauteurs entre 1 et 2 kHz, même lorsque toutes les harmoniques étaient filtrées pour être au-dessus de 6 kHz, et étaient suffisamment résolues pour qu'aucun indice d'enveloppe temporelle ne soit disponible (Oxenham et al., 2011). Ce résultat conduit à une dissociation intéressante : les tons supérieurs à 6 kHz ne produisent pas à eux seuls une hauteur de son utile sur le plan musical ; cependant, ces mêmes tons, lorsqu'ils sont combinés avec d'autres dans une série harmonique, peuvent produire une hauteur de son musicale suffisante pour transmettre une mélodie. Les résultats suggèrent que la limite supérieure de la hauteur musicale ne peut pas être expliquée par la limite supérieure du verrouillage de phase : le fait que la hauteur puisse être entendue même lorsque tous les tons sont supérieurs à 5 kHz suggère soit que l'information temporelle n'est pas nécessaire pour la hauteur musicale, soit que le verrouillage de phase utilisable dans le nerf auditif humain s'étend à des fréquences beaucoup plus élevées qu'on ne le croit actuellement (Heinz, Colburn, & Carney, 2001 ; Moore & Sęk, 2009).

Une autre ligne de preuves de l'importance des informations de lieu provient d'études qui ont examiné la relation entre la précision de la hauteur et les largeurs de bande du filtre auditif. Moore et Peters (1992) ont étudié la relation entre les largeurs de bande du filtre auditif, mesurées à l'aide de techniques de masquage spectral (Glasberg & Moore, 1990), la discrimination fréquentielle en sons purs et la discrimination F0 en sons complexes chez des personnes jeunes et âgées ayant une audition normale et déficiente. Les personnes malentendantes ont été testées parce que la largeur de bande de leur filtre auditif est souvent plus large que la normale. Les résultats sont très variés : certains participants ayant une largeur de bande de filtrage normale ont présenté des seuils de discrimination de la hauteur des sons purs et complexes, tandis que d'autres ayant des filtres anormalement larges présentaient des seuils de discrimination de la hauteur des sons purs relativement normaux. Cependant, aucun des participants dont les filtres auditifs étaient élargis ne présentait des seuils de discrimination F0 normaux, ce qui suggère que des filtres plus larges entraînent peut-être une diminution ou une absence d'harmoniques résolues et que les harmoniques résolues sont nécessaires à une discrimination F0 précise.

Cette question a été approfondie ultérieurement par Bernstein et Oxenham (2006a, 2006b), qui ont systématiquement augmenté l'harmonique la plus basse présente dans un son complexe harmonique et ont mesuré le point auquel les seuils de discrimination F0 se sont détériorés. Chez les auditeurs normo-entendants, il y a une transition assez abrupte d'une bonne à une mauvaise discrimination de la hauteur du son lorsque l'harmonique le plus bas présent est augmenté de la 9ème à la 12ème (Houtsma & Smurzynski, 1990). Bernstein et Oxenham ont pensé que si le point de transition est lié à la sélectivité en fréquence et à la capacité de résolution des harmoniques, alors le point de transition devrait diminuer vers des nombres d'harmoniques plus faibles à mesure que les filtres auditifs s'élargissent. Ils ont testé cette hypothèse chez des auditeurs malentendants et ont trouvé une corrélation significative entre le point de transition et la largeur de bande estimée des filtres auditifs (Bernstein & Oxenham, 2006b), ce qui suggère que les harmoniques doivent être résolues afin d'obtenir une hauteur musicale forte.

Il est intéressant de noter que, même si les harmoniques résolues sont nécessaires à une perception précise de la hauteur, elles ne sont peut-être pas suffisantes. Bernstein et Oxenham (2003) ont augmenté le nombre d'harmoniques résolues disponibles pour les auditeurs en présentant des harmoniques alternées à des oreilles opposées. De cette façon, l'espacement entre les composantes successives dans chaque oreille était doublé, doublant ainsi le nombre d'harmoniques résolues de façon périphérique. Les auditeurs étaient capables d'entendre environ deux fois plus d'harmoniques dans cette nouvelle condition, mais cela n'a pas amélioré leurs seuils de discrimination de hauteur pour le son complexe.

En d'autres termes, le fait de donner accès à des harmoniques qui ne sont pas normalement résolues n'améliore pas les capacités de perception de la hauteur. Ces résultats sont cohérents avec les théories qui reposent sur les modèles de hauteur. Si les harmoniques ne sont pas normalement disponibles pour le système auditif, il est peu probable qu'elles soient incorporées dans les modèles et on ne s'attendrait donc pas à ce qu'elles contribuent à la perception de la hauteur du son lorsqu'elles sont présentées par des moyens artificiels, par exemple en les présentant à des oreilles alternées.

La plupart des sons de notre monde, y compris ceux produits par les instruments de musique, ont tendance à avoir plus d'énergie aux basses fréquences qu'aux hautes ; en moyenne, l'amplitude spectrale diminue à un taux d'environ 1/f, soit -6 dB/octave. Il est donc logique que le système auditif se base sur les harmoniques les plus basses pour déterminer la hauteur du son, car ce sont celles qui sont les plus susceptibles d'être audibles. En outre, les harmoniques résolues - celles qui produisent un pic dans le schéma d'excitation et suscitent une réponse temporelle sinusoïdale - sont beaucoup moins sensibles aux effets de la réverbération de la pièce que les harmoniques non résolues. Les seuils de discrimination de la hauteur pour les harmoniques non résolues sont relativement bons (~2%) lorsque toutes les composantes ont la même phase de départ (comme dans un flux d'impulsions). Cependant, les seuils sont bien pires lorsque les relations de phase sont brouillées, comme ce serait le cas dans une salle ou une église réverbérante, et les seuils de discrimination des auditeurs peuvent être aussi faibles que 10 %, soit plus d'un demi-ton musical. En revanche, la réponse aux harmoniques résolues n'est pas matériellement affectée par la réverbération : le changement de la phase de départ d'une sinusoïde unique n'affecte pas sa forme d'onde - elle reste une sinusoïde, avec des seuils de discrimination de fréquence nettement inférieurs à 1 %.

Un certain nombre d'études physiologiques et de neuro-imagerie ont recherché des représentations de la hauteur tonale au-delà de la cochlée (Winter, 2005). Des corrélations potentielles de la périodicité ont été trouvées dans des études mono- et multi-unités du noyau cochléaire (Winter, Wiegrebe, & Patterson, 2001), dans le colliculus inférieur (Langner & Schreiner, 1988), et dans le cortex auditif (Bendor & Wang, 2005).

Des études de neuro-imagerie humaine ont également trouvé des corrélats de périodicité dans le tronc cérébral (Griffiths, Uppenkamp, Johnsrude, Josephs, & Patterson, 2001) ainsi que dans les structures corticales auditives (Griffiths, Buchel, Frackowiak, & Patterson, 1998). Plus récemment, Penagos, Melcher et Oxenham (2004) ont identifié une région du cortex auditif humain qui semblait sensible au degré de saillance de la hauteur, par opposition aux paramètres physiques, tels que F0 ou la région spectrale. Cependant, ces études ne sont pas non plus exemptes de controverses. Par exemple, Hall et Plack (2009) n'ont pas trouvé de région unique dans le cortex auditif humain qui réponde à la hauteur du son, indépendamment des autres paramètres du stimulus. De même, dans une étude physiologique du cortex auditif du furet, Bizley, Walker, Silverman, King et Schnupp (2009) ont constaté un codage interdépendant de la hauteur, du timbre et de l'emplacement spatial et n'ont pas trouvé de région spécifique à la hauteur.

En résumé, la hauteur des sons complexes mono-harmoniques est déterminée principalement par les 5 à 8 premières harmoniques, qui sont aussi celles que l'on pense être résolues dans le système auditif périphérique. Pour extraire la hauteur, le système auditif doit d'une manière ou d'une autre combiner et synthétiser les informations provenant de ces harmoniques. La manière exacte dont cela se produit dans le système auditif reste un sujet de recherche en cours.

C. Timbre

La définition officielle du timbre selon l'ANSI est la suivante : "L'attribut de la sensation auditive qui permet à un auditeur de juger que deux sons non identiques, présentés de façon similaire et ayant la même intensité sonore et la même hauteur, sont dissemblables" (ANSI, 1994). La norme poursuit en indiquant que le timbre dépend principalement du spectre de fréquences du son, mais peut également dépendre de la pression acoustique et des caractéristiques temporelles. En d'autres termes, tout ce qui n'est pas la hauteur ou la sonie est du timbre. Le timbre faisant l'objet d'un chapitre à part entière dans cet ouvrage (chapitre 2), nous n'en parlerons pas davantage ici. Cependant, le timbre fait une apparition dans la section suivante, où son influence sur les jugements de hauteur et de sonorité est abordée.

D. Interactions sensorielles et influences intermodales

Les sensations auditives de sonie, de hauteur et de timbre sont pour la plupart étudiées indépendamment. Néanmoins, un nombre important de preuves suggère que ces dimensions sensorielles ne sont pas strictement indépendantes. En outre, d'autres modalités sensorielles, en particulier la vision, peuvent avoir des effets considérables sur les jugements auditifs des sons musicaux.

1. Interactions entre la hauteur et le timbre

La hauteur et le timbre sont les deux dimensions les plus susceptibles d'être confondues, notamment par les personnes sans formation musicale. L'augmentation de la F0 d'un son complexe entraîne une augmentation de la hauteur, tandis que la modification du centre de gravité spectral du son augmente sa luminosité - un aspect du timbre (figure 5). Dans les deux cas, lorsqu'on leur demande de décrire le changement, de nombreux auditeurs répondent simplement que le son est "plus aigu".

Figure 5 Représentations de F0 et du pic spectral, qui affectent principalement les sensations de hauteur et de timbre, respectivement.

En général, les auditeurs ont du mal à ignorer les changements de timbre lorsqu'ils jugent de la hauteur. De nombreuses études ont montré que le JND pour F0 augmente lorsque les deux sons à comparer varient également en contenu spectral (par exemple, Borchert, Micheyl, & Oxenham, 2011 ; Faulkner, 1985 ; Moore & Glasberg, 1990). En principe, cela pourrait être dû au fait que le changement de forme spectrale affecte réellement la hauteur ou que les auditeurs ont des difficultés à ignorer les changements de timbre et à se concentrer uniquement sur la hauteur. Les études utilisant l'appariement des hauteurs ont généralement montré que les sons complexes harmoniques sont mieux appariés avec une fréquence en son pur correspondant à la F0, indépendamment du contenu spectral du son complexe (par exemple, Patterson, 1973), ce qui signifie que les effets néfastes des différences de timbre peuvent être liés davantage à un effet de "distraction" qu'à un véritable changement de hauteur (Moore & Glasberg, 1990).

2. Effets des changements de hauteur ou de timbre sur l'exactitude des jugements de sonie
De la même manière que les auditeurs ont plus de difficultés à évaluer la hauteur du son face à un timbre variable, les comparaisons de la sonie entre deux sons deviennent beaucoup plus difficiles lorsque la hauteur ou le timbre des deux sons diffèrent. Par exemple, il est difficile de comparer la sonie entre deux sons purs de fréquence différente (Gabriel et al., 1997 ; Oxenham & Buus, 2000), et de comparer la sonie entre des sons de durée différente, même s'ils ont la même fréquence (Florentine, Buus, & Robinson, 1998).

3. Influences visuelles sur les attributs auditifs
Comme le savent tous ceux qui ont observé un musicien virtuose, l'apport visuel affecte l'expérience esthétique du public. Des influences plus directes de la vision sur les sensations auditives, et vice versa, ont également été signalées ces dernières années. Par exemple, un bruit présenté simultanément avec une lumière a tendance à être jugé plus fort qu'un bruit présenté sans lumière (Odgaard, Arieh, & Marks, 2004). Il est intéressant de noter que cet effet semble être de nature sensorielle, plutôt qu'un effet décisionnel " tardif " ou un changement de critère ; en revanche, des effets similaires du bruit sur la luminosité apparente de la lumière (Stein, London, Wilkinson, & Price, 1996) semblent provenir de mécanismes décisionnels et critériels de plus haut niveau (Odgaard, Arieh, & Marks, 2003). D'autre part, de récentes combinaisons de techniques comportementales et de neuro-imagerie ont suggéré que la combinaison du son et de la lumière peut entraîner une sensibilité accrue à la lumière de faible niveau, ce qui se traduit par des changements dans l'activation des cortex sensoriels (Noesselt et al., 2010).

Les indices visuels peuvent également affecter d'autres attributs du son. Par exemple, Schutz et ses collègues (Schutz & Kubovy, 2009 ; Schutz & Lipscomb, 2007) ont montré que les gestes effectués lors d'une performance musicale peuvent affecter la durée perçue d'un son musical : un geste court ou "staccato" par un joueur de marimba a conduit à des durées jugées plus courtes du son qu'un geste long par le joueur, même si le son lui-même était identique. Il est intéressant de noter que cela ne s'applique pas aux sons soutenus, comme ceux de la clarinette, pour lesquels les informations visuelles ont beaucoup moins d'impact sur les jugements de durée. Cette différence peut être liée à la décroissance exponentielle des sons percussifs, qui n'ont pas de fin clairement définie, ce qui permet aux auditeurs de modifier leur critère pour le point final afin de mieux correspondre aux informations visuelles.

III. Perception des combinaisons de sons

A. Perception et groupement d'objets

Lorsqu'un son musical, tel qu'une note de violon ou une voyelle chantée, est présenté, nous entendons normalement un seul son avec une seule hauteur, même si la note est en réalité constituée de nombreux sons purs différents, chacun ayant sa propre fréquence et hauteur. Cette "fusion perceptive" s'explique en partie par le fait que tous les sons purs commencent et se terminent à peu près en même temps, et en partie par le fait qu'ils forment une seule série harmonique (Darwin, 2005). L'importance de la synchronisation du début et de la fin peut être démontrée en retardant l'une des composantes par rapport à toutes les autres.

Un retard de seulement quelques dizaines de millisecondes est suffisant pour que la composante retardée " ressorte " et soit entendue comme un objet distinct.

De même, si un composant est mal accordé par rapport au reste du complexe, il sera entendu comme un objet distinct, à condition que le déséquilibre soit suffisamment important. Pour les harmoniques à faible numérotation, il suffit de désaccorder une harmonique de 1 à 3 % pour qu'elle " ressorte " (Moore, Glasberg, & Peters, 1986). Il est intéressant de noter qu'une harmonique mal accordée peut être entendue séparément, mais qu'elle peut quand même contribuer à la hauteur globale du complexe ; en fait, une seule harmonique mal accordée continue de contribuer à la hauteur globale du complexe, même si elle est mal accordée de 8 % - bien au-dessus du seuil d'audition d'un objet séparé (Darwin & Ciocca, 1992 ; Darwin, Hukin, & al-Khatib, 1995 ; Moore et al., 1985). Il s'agit d'un exemple d'échec de " l'attribution disjointe " - une composante unique n'est pas attribuée de manière disjointe à un seul objet auditif (Liberman, Isenberg, & Rakerd, 1981 ; Shinn-Cunningham, Lee, & Oxenham, 2007).

B. Percevoir des hauteurs multiples

Combien de sons pouvons-nous entendre en même temps ? Si l'on considère tous les instruments d'un orchestre, on pourrait s'attendre à ce que ce nombre soit assez élevé, et un chef d'orchestre bien entraîné sera souvent capable d'entendre une fausse note jouée par un seul instrument de cet orchestre. Mais sommes-nous conscients de toutes les hauteurs présentées en même temps, et pouvons-nous les compter ? Huron (1989) a suggéré que le nombre de "voix" indépendantes que nous pouvons percevoir et compter est en fait assez faible. Huron (1989) a utilisé des sons de timbre homogène (notes d'orgue) et a fait écouter aux participants des sections d'un morceau de musique d'orgue polyphonique de J. S. Bach avec entre une et cinq voix jouant simultanément. Malgré le fait que la plupart des participants avaient une formation musicale, leur capacité à juger avec précision du nombre de voix présentes diminuait considérablement lorsque le nombre de voix réellement présentes dépassait trois.

En utilisant des stimuli beaucoup plus simples, consistant en plusieurs sons purs simultanés, Demany et Ramos (2005) ont fait la découverte intéressante que les participants ne pouvaient pas dire si un certain ton était présent ou absent de l'accord, mais qu'ils remarquaient si sa fréquence était modifiée lors de la présentation suivante. En d'autres termes, les auditeurs ont détecté un changement dans la fréquence d'un son qui n'avait pas été détecté. Associées aux résultats de Huron (1989), ces données suggèrent que les hauteurs de plusieurs sons peuvent être traitées simultanément, mais que les auditeurs peuvent n'être conscients que d'un sous-ensemble de trois à quatre sons à un moment donné.

C. Le rôle de la sélectivité en fréquence dans la perception de tonalités multiples

1. Rugosité

Lorsque deux sons purs de fréquence différente sont additionnés, la forme d'onde résultante fluctue en amplitude à un rythme correspondant à la différence entre les deux fréquences. Ces fluctuations d'amplitude, ou "battements", sont illustrées à la figure 6, qui montre comment les deux sons sont parfois en phase, et s'additionnent de manière constructive (A), et parfois déphasés, et s'annulent donc (B). À des fréquences de battement inférieures à environ 10 Hz, nous entendons les fluctuations individuelles, mais dès que la fréquence dépasse environ 12 Hz, nous ne sommes plus capables de suivre les fluctuations individuelles et percevons plutôt un son "rugueux" (Daniel & Weber, 1997 ; Terhardt, 1974a).

Figure 6 Illustration des battements créés par la sommation de deux sinusoïdes de fréquences légèrement différentes. À certains moments, les deux formes d'onde sont en phase et s'additionnent de manière constructive (A) ; à d'autres moments, les deux formes d'onde sont en opposition de phase et leurs formes d'onde s'annulent (B). La forme d'onde résultante fluctue à un rythme correspondant à la différence entre les deux fréquences.

D'après les études sur la rugosité, la perception est maximale à des fréquences d'environ 70 Hz et diminue ensuite. La diminution de la rugosité perçue avec l'augmentation de la fréquence s'explique en partie par le fait que le système auditif devient moins sensible à la modulation au-dessus de 100 à 150 Hz environ, et en partie par les effets du filtrage auditif (Kohlrausch, Fassel, & Dau, 2000) : Si les deux tons ne tombent pas dans le même filtre auditif, l'effet de battement est réduit car les tons n'interagissent pas pour former la forme d'onde complexe ; au lieu de cela (comme pour les harmoniques résolus), chaque ton est représenté séparément dans la périphérie auditive. Par conséquent, la perception des battements dépend dans une large mesure des interactions périphériques dans l'oreille. (Les battements binauraux se produisent également entre des sons présentés à des oreilles opposées, mais ils sont beaucoup moins saillants et sont entendus sur une gamme de différences de fréquence beaucoup plus petite ; voir Licklider, Webster, & Hedlun, 1950).

La perception de la rugosité qui résulte des battements a été utilisée pour expliquer un certain nombre de phénomènes musicaux. Tout d'abord, les accords joués dans les registres inférieurs sonnent généralement "boueux", et la théorie musicale demande que les notes d'un accord soient plus espacées que dans les registres supérieurs. Cela peut s'expliquer en partie par le fait que les filtres auditifs sont relativement plus larges aux basses fréquences (en dessous de 500 Hz environ), ce qui entraîne des interactions périphériques plus fortes, et donc une plus grande rugosité, pour les sons qui sont espacés d'un intervalle musical constant. Deuxièmement, on a émis l'hypothèse que la rugosité sous-tend en partie l'attribut de dissonance qui est utilisé pour décrire les combinaisons désagréables de notes. La relation entre la dissonance et le battement est examinée plus en détail dans la section III, D.

2. Perception de la hauteur des sons multiples

Malgré le rôle important des combinaisons de sons ou des accords dans la musique, relativement peu d'études psychoacoustiques ont examiné leur perception. Beerends et Houtsma (1989) ont utilisé des sons complexes composés de seulement deux harmoniques consécutifs chacun. Bien que la hauteur de ces complexes à deux composantes soit relativement faible, avec de la pratique, les auditeurs peuvent apprendre à identifier avec précision la F0 de tels complexes. Beerends et Houtsma ont constaté que les auditeurs étaient capables d'identifier les hauteurs des deux sons complexes, même si les harmoniques d'un même son étaient présentées à des oreilles différentes. La seule exception était lorsque toutes les composantes étaient présentées à une oreille et qu'aucune des quatre composantes n'était considérée comme "résolue". Dans ce cas, les auditeurs n'étaient pas en mesure d'identifier l'une ou l'autre des hauteurs avec précision.

Carlyon (1996) a utilisé des complexes de sons harmoniques avec plus d'harmoniques et les a filtrés de façon à ce que leurs enveloppes spectrales se chevauchent complètement. Il a constaté que lorsque les deux complexes étaient composés d'harmoniques résolus, les auditeurs étaient capables d'entendre la hauteur d'un complexe en présence de l'autre. Cependant, il a été surprenant de constater que lorsque les deux complexes ne comprenaient que des harmoniques non résolues, les auditeurs n'entendaient pas du tout la hauteur du son, mais décrivaient le percept comme un "craquement" non musical. Pour éviter toute ambiguïté, Carlyon (1996) a utilisé des harmoniques qui étaient soit hautement résolues, soit hautement non résolues. Pour cette raison, il n'était pas clair si c'est la résolvabilité des harmoniques avant ou après le mélange des deux sons qui détermine si chaque ton provoque une hauteur claire. Micheyl et ses collègues se sont penchés sur cette question, en utilisant diverses combinaisons de région spectrale et de F0 pour faire varier la résolvabilité relative des composantes (Micheyl, Bernstein, & Oxenham, 2006 ; Micheyl, Keebler, & Oxenham, 2010). En comparant les résultats à des simulations de filtrage auditif, ils ont constaté qu'une bonne discrimination de la hauteur du son n'était possible que lorsqu'au moins deux des harmoniques du son cible étaient considérées comme résolues après avoir été mélangées à l'autre son (Micheyl et al., 2010). Les résultats sont cohérents avec les théories de la hauteur qui reposent sur les harmoniques résolues ; toutefois, il pourrait être possible d'adapter les modèles de hauteur basés sur le temps pour expliquer le phénomène de la même manière (par exemple, Bernstein & Oxenham, 2005).

D. Consonance et dissonance

La question de savoir comment certaines combinaisons de sons sonnent lorsqu'elles sont jouées ensemble est au cœur de nombreux aspects de la théorie musicale. Les combinaisons de deux tons qui forment certains intervalles musicaux, comme l'octave et la quinte, sont généralement considérées comme agréables ou consonantes, tandis que d'autres, comme la quarte augmentée (triton), sont souvent considérées comme désagréables ou dissonantes. Ces types de perceptions impliquant des sons présentés indépendamment d'un contexte musical ont été appelés consonance ou dissonance sensorielle. Le terme de consonance musicale (Terhardt, 1976, 1984) englobe les facteurs sensoriels, mais aussi de nombreux autres facteurs qui contribuent à déterminer si une combinaison de sons est jugée consonante ou dissonante, notamment le contexte (les sons qui l'ont précédée), le style de musique (par exemple, le jazz ou la musique classique), et probablement aussi les goûts personnels et l'histoire musicale de l'auditeur.

La recherche des corrélats acoustiques et physiologiques de la consonance et de la dissonance ne date pas d'hier, puisqu'elle remonte aux observations de Pythagore selon lesquelles les cordes dont les longueurs étaient liées par un petit rapport numérique (par exemple, 2:1 ou 3:2) sonnaient agréablement ensemble. Helmholtz (1885/1954) a suggéré que la consonance pouvait être liée à l'absence de battements (perçus comme une rugosité) dans les sons musicaux. Plomp et Levelt (1965) ont approfondi cette idée en montrant que le classement par consonance des intervalles musicaux au sein d'une octave était bien prédit par le nombre de paires de composants au sein des deux sons complexes qui tombaient dans les mêmes filtres auditifs et provoquaient donc des battements audibles (voir également Kameoka & Kuriyagawa, 1969a, 1969b). Lorsque deux sons complexes forment un intervalle consonant, tel qu'une octave ou une quinte, les harmoniques sont soit exactement coïncidentes, et ne produisent donc pas de battements, soit sont si espacées qu'elles ne produisent pas de battements forts. En revanche, lorsque les tons forment un intervalle dissonant, comme une seconde mineure, aucune des composantes ne coïncide, mais beaucoup sont suffisamment proches pour produire des battements.

Une autre théorie alternative de la consonance est basée sur l'"harmonicité" de la combinaison de sons, ou sur sa ressemblance avec une série harmonique unique. Considérons, par exemple, deux sons complexes qui forment l'intervalle d'une quinte parfaite, avec des F0 de 440 et 660 Hz. Toutes les composantes des deux tons sont des multiples d'un seul F0-220 Hz - et donc, selon la théorie de l'harmonique de la consonance, elles devraient être consonantes. En revanche, les harmoniques de deux tons qui forment une quarte augmentée, avec des F0 de 440 Hz et 622 Hz, ne se rapprochent d'aucune série harmonique unique dans la gamme des hauteurs audibles et devraient donc sonner de manière dissonante, comme cela a été constaté empiriquement. La théorie de l'harmonicité de la consonance peut être mise en œuvre en utilisant un modèle spectral (Terhardt, 1974b) ou en utilisant des informations temporelles, dérivées par exemple de pointes dans le nerf auditif (Tramo, Cariani, Delgutte, & Braida, 2001).

Étant donné que les théories de la consonance et de la dissonance fondées sur le battement et l'harmonique produisent des prédictions très similaires, il a été difficile de les distinguer expérimentalement. Une étude récente a fait un pas vers cet objectif en examinant les différences individuelles dans un grand groupe (>200) de participants (McDermott, Lehr, & Oxenham, 2010). Tout d'abord, on a demandé aux auditeurs de donner des notes de préférence pour des stimuli "diagnostiques" dont le rythme varie mais pas l'harmonique, ou vice versa. Ensuite, les auditeurs devaient indiquer leurs préférences pour diverses combinaisons de sons musicaux, y compris des dyades (accords de deux notes) et des triades (accords de trois notes), en utilisant des instruments de musique et des voix naturels et artificiels. Lorsque les évaluations des deux types de tâches ont été comparées, les corrélations entre les évaluations des tests de diagnostic de l'harmonicité et les sons musicaux étaient significatives, mais les corrélations entre les évaluations des tests de diagnostic du battement et les sons musicaux ne l'étaient pas. Il est intéressant de noter que le nombre d'années de formation musicale formelle est également corrélé avec les évaluations de l'harmonicité et des préférences musicales, mais pas avec les évaluations des battements. Dans l'ensemble, les résultats suggèrent que l'harmonicité, plutôt que l'absence de battement, sous-tend les préférences des auditeurs en matière de consonance et que la formation musicale peut amplifier la préférence pour les relations harmoniques.

Des études sur le développement ont montré que les nourrissons, dès l'âge de 3 ou 4 mois, montrent une préférence pour les intervalles musicaux consonants plutôt que dissonants (Trainor & Heinmiller, 1998 ; Zentner & Kagan, 1996, 1998). Cependant, on ne sait pas encore si les nourrissons réagissent davantage aux battements ou à l'inharmonicité, ou aux deux. Il serait intéressant de découvrir si les préférences des adultes en matière d'harmonicité révélées par McDermott et al. (2010) sont partagées par les nourrissons, ou si les nourrissons fondent initialement leurs préférences sur les battements acoustiques.

IV. Conclusions et perspectives

Bien que la perception des sons musicaux doive être envisagée principalement dans des contextes musicaux, il est possible d'en apprendre beaucoup sur les interactions entre l'acoustique, la physiologie auditive et la perception grâce à des expériences psychoacoustiques utilisant des stimuli et des procédures relativement simples. Des découvertes récentes utilisant la psychoacoustique, seule ou en combinaison avec la neurophysiologie et la neuroimagerie, ont élargi nos connaissances sur la façon dont la hauteur, le timbre et la sonie sont perçus et représentés neuralement, à la fois pour les sons isolés et en combinaison. Cependant, il reste encore beaucoup à découvrir. Parmi les tendances importantes, citons l'utilisation de stimuli plus naturels dans les expériences et pour tester les modèles informatiques de perception, ainsi que la combinaison simultanée de mesures perceptives et neurales pour tenter d'élucider les mécanismes neuraux sous-jacents de la perception auditive. En utilisant les éléments de base fournis par la psychoacoustique des sons musicaux individuels et simultanés, il est possible de répondre à des questions beaucoup plus sophistiquées concernant la perception de la musique lorsqu'elle se déroule dans le temps. Ces questions et d'autres sont abordées dans les autres chapitres de ce volume.

Remerciements
Emily Allen, Christophe Micheyl et John Oxenham ont fourni des commentaires utiles sur une version antérieure de ce chapitre. Les travaux du laboratoire de l'auteur bénéficient du soutien financier du National Institutes of Health (subventions R01 DC 05216 et R01 DC 07657).